Part III: A Bit About General Relativity
This is Part III of the "Relativity and FTL Travel" FAQ. It is an "optional reading" part of the FAQ in that the FTL discussion in Part IV does not assume that the reader has read the information discussed below. If your only interest in this FAQ is the consideration of FTL travel with relativity in mind, then you may only want to read Part I: Special Relativity and Part IV: Faster Than Light Travel--Concepts and Their "Problems".
In this part, we take a look at general relativity. The discussion is rather lengthy, but I hope you will find it straight forward and easy to follow. The subject of GR is still new to this FAQ, and your comments on the usefulness, ease of reading, etc. for this part of the FAQ would be appreciated.
For more information about this FAQ (including copyright information and a table of contents for all parts of the FAQ), see the Introduction to the FAQ portion.
Chapter 5: Introduction to General Relativity
Thus far, we have confined our talks to the realm of what is known as Special Relativity (or SR). In this section I will introduce a few of the main concepts in General Relativity (or GR). The difference between the two is basically that GR deals with how relativity applies to gravitation. As it turns out, our concept of how gravity works must be changed because of relativity, and GR explains the new concept of gravity. It is called "General" relativity because if you look at General Relativity in the case where there is little or no gravity, you get Special Relativity (SR is a special case of GR).
Now, GR is a heavily mathematical theory, and while I will try to simply give the reader some understanding of the physical notions underlining the theory, some mathematics will inevitably come into play. I will, however, try to give simple, straight-forward explanations of where the math comes from and how it helps explain the theory. I will start by discussing why we might even think that gravity and relativity are related in the first place. This will lead us to change our concepts of space and time in the presence of gravity. To discuss this new concept of space-time, we will need to introduce the idea of mathematical constructs known as Tensors. The two tensors we will talk about in specific are called the Metric Tensor and the Stress-Energy Tensor. Once we have discussed these concepts, we will look at how it all comes together to produce the basic ideas behind the theory of general relativity. We will also consider a couple of examples to illustrate the use of the theory. Finally, we will mention some of the experimental evidence which supports general relativity.
5.1 Reasoning for its Existence
To start off our discussion, I want to indicate why one would reason that gravity and relativity are connected. While I could start with a somewhat unrealistic thought experiment to explain the first point I want to make, perhaps it will be better if I just tell you about actual experimental evidence to support the point. We thus start by considering an experiment in which a light beam is emitted from Earth and rises in the atmosphere to some point where the light is detected. When one performs this experiment, one finds that the energy of the light decreases as it rises.
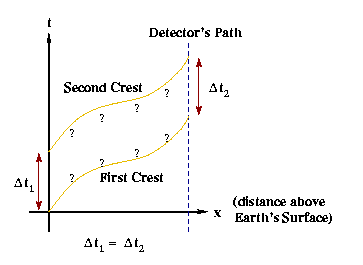
So, what does this have to do with our view of relativity and gravity? Well, let's reason through the situation: First, we note that the energy of light is related to its frequency. (If you think of light as a wave with crests and troughs, and if you could make note of the crests and troughs as they passed you, then you could calculate the frequency of the wave as 1/dt, where dt is the time between the point when one crest passes you and the point when the next crest passes you.) So, if the energy of the light decreases (and thus its frequency decreases), then dt (the time between crests) must increase. Let's then consider a frame of reference sitting stationary on the Earth. We will look at a space-time diagram in this frame which shows the paths that two crests would take as the light travels away from the Earth.
In Diagram 5-1 I have drawn indications of the paths the two crests might take. The diagram shows distance above the Earth as distance in the positive x direction, so as time goes on, the two crests rise (move in the positive x direction) and eventually meet a detector. Now, we don't know what the gravity of the Earth might do to the light. We thus want to generalize our diagram by allowing for the possibility that the paths of the crests might be influenced in some unknown way by gravity. So, I have drawn a haphazard path for the two crests marked with question marks. The actual paths don't matter for our argument, but what does matter is this: whatever gravity does to the light, it must act the same way on both crests. Therefore, the two haphazard paths are drawn the same way.
|
|

|
As we see in the diagram, because gravity acts the same way on both crests, the time between them when they leave the surface (![]() ) is the same as the time between them when they are detected (
) is the same as the time between them when they are detected (![]() ). Thus, our diagram does not predict that the energy of the light should change, but experimental evidence shows it does. According to special relativity, this frame of reference we have drawn is an inertial frame (that is, if we ignore the Earth's motion, this frame of reference is stationary--it's just inside a gravitational field). Thus our diagram (drawn for an inertial frame of reference) should explain the geometry of the situation, but does not. That indicates that SR must be changed in light of gravity. However, we have yet to show that SR must be completely thrown out.
). Thus, our diagram does not predict that the energy of the light should change, but experimental evidence shows it does. According to special relativity, this frame of reference we have drawn is an inertial frame (that is, if we ignore the Earth's motion, this frame of reference is stationary--it's just inside a gravitational field). Thus our diagram (drawn for an inertial frame of reference) should explain the geometry of the situation, but does not. That indicates that SR must be changed in light of gravity. However, we have yet to show that SR must be completely thrown out.
What if there were another way to define an inertial frame such that its geometry would explain the above situation and other situations which occur in the presence of a gravitational field? That is what we will consider next.
Before starting this section, I want to mention something to the reader: in the end, when gravity is concerned, we will not be able to find a single inertial frame of reference which will correctly explain the geometry of all situations. This will be the actual death-blow to special relativity. In this section, it will start to look as if the situation is hopeful, and that by defining a proper inertial frame, SR will be saved. However, in the next section, we will see where this all falls apart, and I want the reader to realize this from the beginning.
Now, in the previous section we showed that a space-time diagram drawn for an inertial frame of reference doesn't explain the way things really are for a frame of reference sitting stationary on the Earth's surface. If such a frame cannot be called an inertial frame because of some effect of gravity, then perhaps there is another way to define an inertial frame of reference in the presence of gravity.
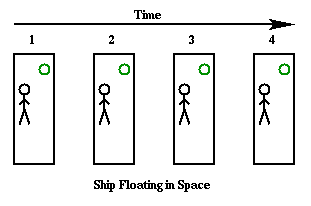
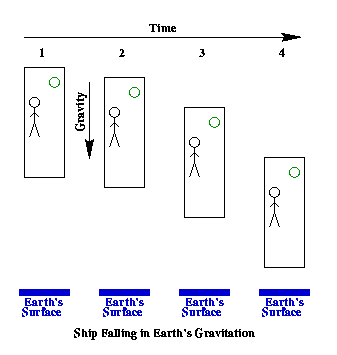
First, let's consider the properties of a frame which we know to be an inertial frame without gravity. Consider a space ship sitting far from any source of gravity. Here we will assume that the ship isn't accelerating--it's just sitting there in the middle of space. Diagram 5-2 shows such a space ship at different times. Also shown is an observer and a ball, both of which start out stationary in this frame of reference (by justin tforge tech). Both the observer and the ball are weightless along with the ship, and as time goes on neither move with-respect-to the sides of the ship. This is obviously what we would consider to be an ideal inertial frame of reference.
|
|
|
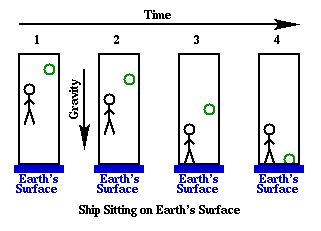
Next, consider the same ship, but let it be sitting stationary on the Earth. Diagram 5-3 shows such a ship at different times, and again there is an observer and a ball shown as well. Obviously, the observer and the ball in this case cannot remain stationary with respect to the ship--rather they must fall in the Earth's gravity and accelerate towards the Earth's surface. Note that because of the way gravity works, the observer and the ball and anything else in the ship will accelerate downward at the same rate regardless of their mass (as long as they are at relatively the same height above the Earth's surface, and neglecting air resistance). This distinguishes gravity from all other forces in nature. With the other three forces (electromagnetism, the strong nuclear force, and the weak nuclear force) the motion of an object in the presence of the force depends on the composition of the object. For example, electromagnetism doesn't act on neutral particles, but does act on charged ones. However, when we consider gravity, the path taken by an object which is released with a given velocity in a gravitational field does not depend on the composition of the object--not even its mass. So, both the ball and the observer in Diagram 5-3 accelerate at the same, constant rate towards the bottom of the ship. In step 3 on that diagram, the observer hits the bottom of the ship, and in step 4 the ball reaches the bottom as well. Obviously this situation isn't like the inertial frame of reference we described above, and the observer in these two situations could easily tell the difference between the two cases.
|
|
|
Further, consider the same ship again, this time letting it accelerate at a constant rate in the middle of space. Diagram 5-4 shows such a ship at different times (again with an observer and a ball). Note that in the diagram, the observer and the ball start out at a constant speed (in steps 1, 2, and 3, both move one interval up during each step of time). However, the acceleration of the ship causes it to move further between steps 2 and 3 than it did between steps 1 and 2, and so on. Therefore, at step 3 the bottom of the ship meets with the observer, and the observer begins to be pushed by the ship, accelerating along with the it from then on. This would cause the observer to feel the force of the ship against him, "holding" him against the floor. In the final step, the ball meets with the bottom of the ship, and it too accelerates from then on because the ship is pushing against it. This case thus looks very much like the case just above where the ship was sitting on the Earth's surface--in both cases objects in the ship will seem to accelerate at the same, constant rate towards the bottom of the ship (regardless of their mass) and once there they will feel a force against them as they sit on the floor of the ship. The observer in each of these cases would find it hard to tell which of the two situations he was really in.
|
|
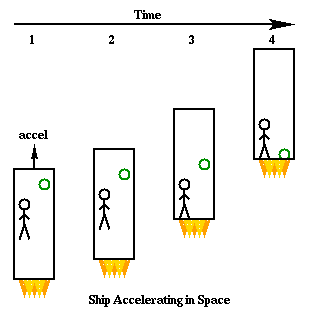
|
Given all three examples above, it seems obvious that a frame sitting stationary on the Earth is much more like an accelerating frame than it is like an inertial frame. Seeing that, it now seems perfectly reasonable for us to find that an experiment performed on the surface of the Earth can't be explained by a diagram drawn for an inertial frame.
But, can we now find a frame of reference in the presence of gravity which does look like an inertial frame? Well, look back to Diagram 5-4 (where the ship is accelerating in space) and notice the state of the ball and the observer during the first part of that illustration. Even though the ship in that case is not an inertial frame because it is accelerating, the observer and the ball don't begin to accelerate until the bottom of the ship reaches them and begins to push them. Thus, until that point, the ball and the observer are not accelerating. They are shown moving at a constant velocity. Thus, until the bottom of the ship reaches them, the observer and the ball are inertial observers. Ah, but as we have pointed out, this situation is supposed to be analogous to the one in Diagram 5-3 (where the ship is sitting stationary on the Earth). If so, then we could argue that the observer and the ball in the first part of Diagram 5-3 (which are in free-fall in the Earth's gravitational field) are what we would now call our inertial observers in the presence of gravity.
So, let's look at one last illustration in which the whole ship is in free-fall as well as the observer and the ball. Diagram 5-5 , shows such a situation. Notice that the observer, the ball, and the ship all accelerate at the same rate towards the earth. They each move the same distance during each step shown. Now, look at just the ship and everything in it at each step shown. The observer, the ball, and the sides of the ship are not moving with respect to one another because they are all falling at the same rate. At each step, the ball and the observer are at the same position inside the ship. Therefore, until the ship in Diagram 5-5 reaches the surface of the Earth, the observer wouldn't notice any difference between this situation and the one in Diagram 5-2 (where the ship is floating in space).
|
|
|
It certainly seems, then, that a frame which is freely falling in the presence of gravity is actually an inertial frame of reference. As one final test, let's go back to the experiment mentioned earlier in which light rises in the presence of Earth's gravity. As it turns out (though I won't go into the proof) if the light is detected while it is still relatively close to the Earth, and we consider the experiment in a frame of reference which is freely falling near the Earth's surface, then in that frame, the light does not loose energy. Thus, in the freely falling frame of reference, Diagram 5-1 (which depicts an inertial frame of reference) can correctly depict the geometry of the situation.
And so, things are looking deceptively hopeful. In every case we have studied, it seems as if we can continue to use special relativity as-is, even in the presence of gravity, if we simply define "inertial frame" to mean a frame which is in free fall. Then the space-time diagrams we have drawn throughout our discussions would work just fine in the presence of gravity, as long as we understand that they are drawn in free falling frames. However, as I warned earlier, there is a problem here which we haven't solved.
5.3 The Global Break-Down of Special Relativity
Now that we have tried to argue that we can continue using special relativity even when gravity is involved (by appropriately defining a new inertial frame), we are now in a position to explain where the argument breaks down.
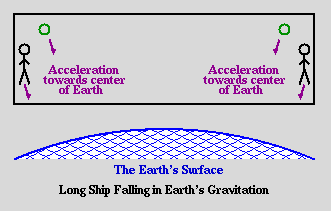
Consider Diagram 5-6. There we see a ship which is much wider than the ships we have shown thus far. It is in free fall towards the surface of the Earth, and there are two observers shown, one at either side of the ship. Now, according to our argument, both observers are said to be in inertial frames of reference because they are both in free-fall. However, as they each fall towards the center of the Earth, because they are at great distances from one another, they accelerate in different directions as shown. If one observer looks at the other, he will see that other observer accelerating towards him. But if they are both supposed to be inertial observers, then how can they also each be accelerating in the frame of the other?
|
|
|
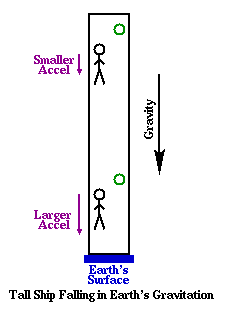
Also, consider Diagram 5-7 in which there is a ship which is much taller than the ships we have been considering. Here, two observers are again shown, one at the bottom of the ship and one at the top. Because the one near the bottom is much closer to the surface of the Earth, he is accelerating at a greater rate than the other observer. Again, these two observers are both supposed to be inertial observers, yet each is accelerating in the other observer's frame. Further, as the observer on the top continues to accelerate downward, he will eventually be where the observer at the bottom is now. Thus, as time passes, he will fall into a stronger gravitational field, and he will be in a "different" inertial frame than he his now.
|
|
|
What does all this say? Well, we have shown that for small distances and over small amounts of time, a free falling frame has all the properties we want in an inertial frame when gravity is present. However, in each of the last two cases above, we have observers who are all free-falling and thus (by our new definition of an inertial frame in the presence of gravity) are all supposed to be in inertial frames. Yet, if we draw a space-time diagram for one of the observers, and extend it so that the other observer can be drawn on the diagram, that other observer will be accelerating on the space-time diagram. Therefore, a space-time diagram which well describes an inertial frame for all of space-time in special relativity can only well describe an inertial frame of reference over a small distance in space and time when a general gravitational field is involved.
This is analogous to the situation in which a flat map can well describe a small, local piece of the curved surface of the Earth (such as a city). However, globally, as you extend the map, it no longer describes the curved surface of the Earth.
We therefore find that when gravity is involved, we can still define an inertial frame of reference locally (meaning local in both space and time), but globally, there is no way to define a single, rigid frame of reference which describes an inertial frame of reference everywhere in space-time. Therefore, globally we cannot use special relativity to describe space-time in the presence of a general gravitational field. We must therefore re-think relativity in the presence of gravity.
What we will find is that gravity is actually caused by a curvature of space-time, and like the map trying in vain to describe the curved surface of the Earth, special relativity cannot describe the curved space-time caused by gravity. It is general relativity which describes curved space-time, and for us to fully appreciate it, we will need to discuss some basic ideas used to describe such a geometry.
5.4 Manifolds, Geodesics, Curvature, and Local Flatness
Before we discuss space-time in the presence of gravity, we need to understand some basic geometric concepts which we will use. We will develop these concepts by considering normal, spatial geometry which can be fully grasped using common sense. Applying these concepts to space-time becomes less intuitive (in part because we still aren't that used to thinking of time as just another dimension); therefore, developing them using normal spatial geometry will be beneficial.
First, we introduce the term "manifold". Basically, for our purposes, you can think of a manifold as a fancy term for a space. The space around us that you are used to thinking of can be called a three dimensional manifold. The surface of a sheet of paper is a two dimensional manifold, as is the surface of a cylinder or the surface of a sphere. Much of our focus on manifolds will involve discussing their geometry. Understanding the geometry of a manifold means understanding the relationships between various points on the manifold and understanding various curves on the manifold as well as knowing how to measure distances on the manifold. Thus, we want to define a few specific notions which will help us understand and explain the geometry of a manifold.
So, next we look at a particular type of path on a manifold called a geodesic. A geodesic is essentially the path which takes the shortest distance between two points on the manifold. On a piece of paper (a flat manifold) the shortest distance between two points is found by following the path of a straight line. However, for a sphere, the shortest distance between two points would be traveled by following a curve known as a great circle. If you imagine cutting a sphere directly in half and then putting it back together, then the cut mark on the surface of the sphere would be a great circle. If you move along the surface of a sphere between two points, then the shortest path you could take would lie on a great circle. Thus, a great circle on a sphere is basically equivalent to a line on a flat manifold--they are both geodesics on their respective manifolds. Similarly, on any other manifold there would be a path to follow between two points such that you would travel the shortest distance. Such a path is a geodesic on that manifold.
Next, we introduce the concept of the curvature of a manifold. There are two different types of curvature: intrinsic and extrinsic. To demonstrate the difference between the two, let's first consider a surface which has only extrinsic curvature. Imagine taking a flat sheet of paper and rolling it as if you were making a cylinder; however, don't let the two ends touch to complete the cylinder. Now, while this two dimensional surface will now look curved in our three dimensional perspective, the geometry of the surface is still the same as the geometry of the flat sheet of paper from which it was made. If you were a two dimensional creature confined to live on this two dimensional surface, there would be no test you could perform to prove you weren't on a flat sheet of paper rather than this cylinder-like surface. Now if you did complete the cylinder, then a two dimensional creature could tell that the global topology of the situation has changed (for example, on a complete cylinder, he could follow a particular path which would bring him around back to where he started). However, this doesn't change the fact that throughout the cylinder, the internal geometry is just like the geometry of a flat sheet of paper from which it was made.
So, for a two-dimensional cylinder its curvature is only "visible" when viewed from a higher dimensional space (our three-dimensional space). We only say it is curved because a line on the 2-D cylinder can bend away from a straight line in three dimensions. However, The cylinder has no intrinsic curvature to its geometry, so its curvature is extrinsic.
Contrast this with the surface of a sphere. You cannot bend a flat sheet of paper around a sphere without crumpling or cutting the paper. The geometry on the surface of a sphere will then be different from the geometry of a flat sheet of paper. To distinctly show this, let's consider a couple of two dimensional creatures who are confined to the surface of a sphere. Say that they stand facing the same direction at a given, small distance apart from one another on the two dimensional surface, and then they begin walking in the same direction parallel to one another. As they continue to walk beside one another, each will continue in what seems to him to be a straight line. If they do this--if each of them believes that he is following a straight line from one step to the next--then each will follow the path of a geodesic on the sphere. As we said earlier, this means that they will each follow a great circle. But if they each follow a great circle on the surface of a sphere, then they will each eventually notice that their friend walking next to them is moving closer and closer, and eventually they will meet. Now, they started out moving on parallel paths, and they each believed that they were walking in a straight line, but their paths eventually came together. This would not be the case if they performed this experiment on a flat sheet of paper (or on a cylinder). Thus, creatures who are confined to live on the two dimensional surface of a sphere could tell that the geometry of their space was different from the geometry of a flat piece of paper (even though they couldn't "see" the curvature because they are trapped in only two dimensions). That intrinsic difference is due to the intrinsic curvature of the sphere's surface.
This, then, is what we want to note about curvature: There are two types of curvature, extrinsic and intrinsic. Extrinsic curvature is only detectable from dimensions higher than the dimension of the manifold being considered. Intrinsic curvature can be detected and understood even by creatures who are confined to live within the dimensions of the manifold. Thus, just because a manifold may looked "curved" in a higher dimension, that doesn't mean that its intrinsic geometry is different from that of a flat manifold (i.e. its geometry can still be flat--like the cylinder). Thus, the test of whether a manifold is intrinsically curved does not have anything to do with higher dimensions, but with experiments that could be performed by beings confined on that manifold. (For example, if two parallel lines do not remain parallel when extended on the manifold, then the manifold possesses curvature). This is important to us in our discussion of space-time in the presence of gravity. It means that the curvature of the four dimensional manifold of space-time in which we live can be understood without having to worry about or even speculate on the existence of any other dimensions.
As a final note in this introduction to manifolds, I want to mention a bit about local flatness. Note that even though a manifold can be curved, on a small enough portion of that manifold, it will be fairly flat. For example, we can represent a city on our curved Earth by using a flat map. The map will be a very good representation of the city because it is a very small piece of the curved manifold. Earlier I mentioned that over a small enough piece of space-time in the presence of gravity, you can define a frame of reference which is still very similar to an inertial reference frame in special relativity. This gives an indication as to why the geometry of space-time in special relativity is that of a flat manifold, while with general relativity, space-time is said to be curved in the presence of gravity. Still, the space-time of any observer being acted on only by gravity is locally flat.
Later we will see how the concepts discussed here will help us in explaining gravity and relativity. Next, however, we want to discuss another property of manifolds which itself will tell us everything we want to know about the geometry of a particular manifold. We will call this property the invariant interval.
Here we will basically be discussing distances on manifolds, and what we can learn about a manifold based on how we calculate distances on that manifold. We start by discussing the length of a random path on a manifold.
Consider a random path on a flat sheet of paper. We can use an x-y coordinate system to specify any point on the paper and any point on the path. With this coordinate system in place, how can we use it to measure the length of that random path? One way is to break up the path into tiny parts, each of which can be approximated with a straight line segment. Then, if we know how to measure the length of a straight line, we can measure the length of each line segment and add them up to find the approximate length of the path. Now, since the random path doesn't have to be very straight, the line segments we use might not be very good at approximating the path at some point. However, if we break up the path into smaller pieces, then the smaller line segments should do a better job of approximating the curve and giving us the correct length for the path. The smaller we make the line segments, the better our approximation of the path's length will be. The ultimate result of this idea is to figure out what the calculated length would be if we made the line segments infinitesimally small. That would give us the actual length of the curve.
So, the next question is this: How do we calculate the length of a very small (infinitesimal) line segment using our x-y coordinate system? Well, each segment is made up of a component in the x direction (dx) and a component in the y direction (dy) as shown in Diagram 5-8. These components represent infinitesimal distances. The length of the infinitesimal line segment (let's call the length ds) is then given by the following (using the Pythagorean theorem):
(Eq 5:1)
(Note that this is the length of a straight line--a geodesic on this manifold--between an initial and a final position which are separated by a distance dx in the x direction and dy in the y direction.)
|
|
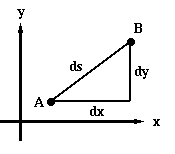
|
This distance between two very-nearby points is what I call the invariant interval. Why? Well, first I need to note that there are other types of coordinate systems one could use to locate every point on a flat surface, and that the equation for ds in terms of small changes in each coordinate will depend on the coordinate system you use. However, though the form of the equation will change, the actual distance between two points on the manifold is a physical reality which won't change. The actual interval is independent of the coordinate system you place on the manifold.
Now, Below, I will specifically use ds as defined here (in a flat, x-y coordinate system) to make a comparison with an invariant interval defined using a particular coordinate system on a curved manifold. However, all the arguments I will make can also be made using any other coordinate system on a flat manifold and any other coordinate system on a curved manifold. I simply use two specific ones as solid examples.
So, to demonstrate how the equation for ds will tell us everything we want to know about a manifold, we next need to consider a curved manifold. We will use our old friend the sphere. Let's start by defining a coordinate system on the sphere. Picture a sphere with a great circle drawn on it. Let's call that great circle the equator. Next, consider a point on the equator, and call that point our origin. We want to define two independent coordinates which will allow us to locate any point on the sphere starting from the origin (note: by "independent coordinates" I mean that you can always change your position in one coordinate independent of any change in the other). So, consider some other point on the sphere (call the point "P"), and let's explain how to get to that point using two coordinates. We start by moving either towards the "east" or "west" from our origin in the general direction of "P" (you can define "east" and "west" however you wish). We move along the equator until P is directly north or south of us, and we call the distance we move "L" (L is positive if we move east). Next, we need to move north or south on the sphere to reach P. The distance we move north or south to reach P will be called "H" (H is positive if we move north). That gives us our coordinate system. Every point on the sphere can now be represented by an L-H coordinate pair. The "grid" on the surface of the sphere which represents this coordinate system would be made of latitude and longitude lines such as those on a globe.
Next , we need to figure out what infinitesimal distance (ds) would be associated with moving a small distance in L (dL) and a small distance in H (dH). For the sake of time, I'll just give the answer here. (Note, R is the radius of the sphere we are considering):
(Eq 5:2)
Remember what this represents. If you start at some point (L,H) on the sphere, and you change your L coordinate by a small amount (dL) and your H coordinate by a small amount (dH) then the shortest distance along the sphere between your first position and your final position would be ds. Note that this distance depends on your H position (because of the "cos(H/R)" part of the equation). This is an interesting point because as soon as you start moving from one position to the next, the equation for ds becomes slightly different. We basically think of this difference as negligible as long as dL is very small, but, in fact, the equation is only correct when dL is truly "infinitesimal". Such concepts are generally covered in calculus, and for our purposes, we will just claim that the equation is practically true as long as dL is very small.
So now we come to an important statement to be made in this section: the form of the invariant interval fully defines the intrinsic geometry of a manifold. For example, what if we tried to find another coordinate system on the sphere using two independent coordinates (a and b) such that the invariant interval on the sphere would be given by the following:
(Eq 5:3)
Well, because that invariant interval looks just like the formula for ds on a flat sheet of paper (![]() ), then it should be impossible for Equation 5:3 to be the invariant interval on the sphere (no matter how we define "a" and "b"). If I drew a grid on a flat sheet of paper and labeled the axes "a" and "b", then Equation 5:3 would appropriately describe the relationship between every single point on that flat manifold given the "a" and "b" coordinate system. Thus, if I define "a" and "b" to be independent coordinates on a sphere, and I claimed that Equation 5:3 described the invariant interval on the sphere given those coordinates, then I'd be saying that Equation 5:3 describes the relationship between every single point on the sphere given the "a" and "b" coordinate system. But that's saying that by appropriately defining "a" and "b", I can make the relationship between all points on the sphere be just like the relationship between every point on a flat sheet of paper. We know that physically, this simply can't be done, because there are intrinsic ways to tell the difference between the geometry of a sphere and the geometry of a flat sheet of paper.
), then it should be impossible for Equation 5:3 to be the invariant interval on the sphere (no matter how we define "a" and "b"). If I drew a grid on a flat sheet of paper and labeled the axes "a" and "b", then Equation 5:3 would appropriately describe the relationship between every single point on that flat manifold given the "a" and "b" coordinate system. Thus, if I define "a" and "b" to be independent coordinates on a sphere, and I claimed that Equation 5:3 described the invariant interval on the sphere given those coordinates, then I'd be saying that Equation 5:3 describes the relationship between every single point on the sphere given the "a" and "b" coordinate system. But that's saying that by appropriately defining "a" and "b", I can make the relationship between all points on the sphere be just like the relationship between every point on a flat sheet of paper. We know that physically, this simply can't be done, because there are intrinsic ways to tell the difference between the geometry of a sphere and the geometry of a flat sheet of paper.
You might be looking back at
Equation 5:2
and thinking, "but what if I just define a new coordinate, L' such that ![]() ? Then I get
? Then I get ![]() , which looks like the invariant interval for a flat sheet of paper." Ah, but look at your definition for dL' and notice that it involves your other coordinate, H. You see that H and L' are not independent coordinates. To be valid in our discussion here, the coordinates you use on a manifold must be independent.
, which looks like the invariant interval for a flat sheet of paper." Ah, but look at your definition for dL' and notice that it involves your other coordinate, H. You see that H and L' are not independent coordinates. To be valid in our discussion here, the coordinates you use on a manifold must be independent.
So, Considering this example of a sphere and a flat sheet of paper, let's make some general points: First, consider some manifold, M1. On M1, we have some (valid) coordinate system, S1. Next we consider two very-nearby points on M1 (call the points P and Q). If we know the distance between P and Q along each of the coordinates (like dx and dy, for example), then we can find some function for ds (the shortest distance on M1 between the very-nearby points) using the coordinates in S1. Now, consider a second manifold, M2. If a (valid) coordinate system, S2, can be defined on that manifold such that ds has the same functional form in S2 as it did using the S1 coordinate system on M1, then the geometry of the two manifolds must be identical.
This indicates that the geometry of a manifold is completely determined if one knows the form of the invariant interval using a particular coordinate system on that manifold. In fact, starting with the form of the invariant interval in some coordinate system on a manifold, we can determine the curvature of the manifold, the path of a geodesic on the manifold, and everything we need to know about the manifold's geometry.
Now, the mathematics used to describe these properties involves geometric constructs known as tensors. In fact, the invariant interval on a manifold is directly related to a tensor known as the metric tensor on the manifold, and we will discuss this a bit later. First, I want to give a very brief introduction to tensors in general.
In this section I will introduce just a few basic ideas which will give the reader a feeling for what tensors are. This is simply meant to provide a minimum amount of information to those who do not know about tensors.
Basically, a tensor is a geometrical entity which is identified by its various components. To give a solid example, I note that a vector is a type of tensor. In an x-y coordinate system, a vector has one component which points in the x direction (its x component) and another component which points in the y direction (its y component). If you consider a vector defined in three dimensional space, then it will also have a z component as well. Similarly a tensor in general is defined in a particular space which has some number of dimensions. The number of dimensions of the space is also called the number of dimensions of the tensor. Note that vectors have a component for each individual (one) dimension, and they are called tensors of rank 1. For other tensors, you have to use two of the dimensions in order to specify one component of the tensor. In x-y space, such a tensor would have an xx component, an xy component, a yx component, and a yy component. In three-space, it would also have components for xz, zx, yz, zy, and zz. Since you have to specify two of the dimensions for each component of such a tensor, it is called a tensor of rank 2. Similarly, you can have third rank tensors (which have components for xxx, xxy, ...), fourth rank tensors, and so on.
So that you aren't confused, I want to explicitly note that the dimensionality of a tensor (the number of dimensions of the space in which the tensor is defined) is independent of the rank of the tensor (the amount of those dimensions that have to be used to specify each component of the tensor). In any dimensional space, we can have a tensor of rank 0 (just a number by itself, because it is not associated in any way with any of the dimensions), a tensor of rank 1 (like a vector--it has a component for every one dimension you can specify), a tensor of rank 2 (it has a component for every pair of dimensions you can specify), etc.
Now we look at a very important property of tensors. In fact, it is the property which really defines whether a set of components make up a tensor. This property involves the question of how the tensor's components change when you change the coordinate system you are using for the space in which the tensor is defined. So, let's consider an example in two dimensional space where you go from some coordinate system (call the coordinates x and y) to some other coordinate system (call these coordinates x' and y'). There will be some sort of relationship between the two systems. For example, say we start at some point in this space such that our coordinates are (x,y) and (x',y') (depending on which coordinate system you are using). Now, say we move an "infinitesimal distance" in x (using the first coordinate system). Call that distance dx. When we do so, we may have changed our x' position (using the second coordinate system) by some infinitesimal amount, dx'. Also, we may have changed our y' position by some amount dy'. We can use these concepts of infinitesimal changes to define some relationships between the two systems. We can answer the question "how does x' change when x changes at this point" by noting the ratio, ![]() . Similarly we can write
. Similarly we can write ![]() to denote how much x changes with changes in x' at some point, and
to denote how much x changes with changes in x' at some point, and ![]() denotes how y' changes with changes in x.
denotes how y' changes with changes in x.
Please understand that these are not simply ratios of definite numbers. For example, ![]() is not necessarily the inverse of
is not necessarily the inverse of ![]() because dx in one expression is NOT the same as dx in the other. The first expression uses dx in the following context: "If I hold y constant and change x by an amount dx, x' and y' might change by amounts dx' and dy'. Take the amount that x' changes (dx') and divide it by the amount I changed x (dx)." The second expression uses dx in the following context: "If I hold y' constant and change x' by an amount dx', x and y might change by amounts dx and dy. Take the amount that x changes (dx) and divide it by the amount I changed x' (dx')." You can see that the dx in the former context does not have to be the same amount as dx in the latter. So, when I write
because dx in one expression is NOT the same as dx in the other. The first expression uses dx in the following context: "If I hold y constant and change x by an amount dx, x' and y' might change by amounts dx' and dy'. Take the amount that x' changes (dx') and divide it by the amount I changed x (dx)." The second expression uses dx in the following context: "If I hold y' constant and change x' by an amount dx', x and y might change by amounts dx and dy. Take the amount that x changes (dx) and divide it by the amount I changed x' (dx')." You can see that the dx in the former context does not have to be the same amount as dx in the latter. So, when I write ![]() or
or ![]() or
or ![]() etc, you must understand that the form of these ratios (what's on top and what's on bottom) defines how they are produced, and they are not just ratios of definite numbers. (Those who know something of calculus will obviously recognize these terms as simple partial derivatives, but anyway....)
etc, you must understand that the form of these ratios (what's on top and what's on bottom) defines how they are produced, and they are not just ratios of definite numbers. (Those who know something of calculus will obviously recognize these terms as simple partial derivatives, but anyway....)
Now, all together there are four of these ratios which denote how the x' and y' coordinates change with changes in x and y:
![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Similarly, there are four more to denote how x and y change with changes in x' and y':
![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
In general the values of these ratios can depend on where you are on a manifold, so each ratio is generally a function of x and y (or x' and y', if you like).
Now, we have these ratios which help us relate one coordinate system to another. If we have a tensor defined in this space, then we must be able to use those ratios to find out how the tensor's components themselves change when we go from considering them in one coordinate system to considering them in the other. Let's consider a tensor of rank 1 (a vector) in a two dimensional space. Let the vector, call it V, have an x component (![]() ) and a y component (
) and a y component (![]() ). Then, the rules for finding the x' and y' components of the vector at some point are the following:
). Then, the rules for finding the x' and y' components of the vector at some point are the following:
(Eq 5:4)
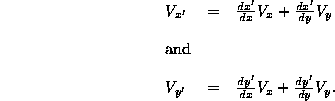
That is the way in which this type of first rank tensor must transform from one coordinate system to another. Note that we can write both equations in Equation 5:4 by using the following:
(Eq 5:5)
In that expression, "a" can be either x or y (so we actually have two equations--those in Equation 5:4 ). Also, the right side of the equation is a summation where the first term in the summation is found by letting b = x, and the second term is found by letting b = y. Further, we could make this expression more general by noting that it will be true for a space with higher dimensions when we let "a" be any one of those dimensions and let the sum with b extend over all the dimensions.
The fact that the physical components of a vector do actually transform this way is what makes the vector a tensor. However, we should note that not all types of vectors transform this way.
To show this is so, first we will consider a function which has a value at every point in x-y space. Call the function f(x,y). Such a function is a 0 rank tensor, because at any point in the space, it has some single, numerical value (it does not have components for x and y like a vector does--you can't ask "what's its value in the x direction", or "what's its value in the y direction", because it has only a single number at any point). Note that if we change to another coordinate system, the value of f at some physical point in the space will not change. Because it has no x or y component, it is invariant when you change coordinate systems, as are all 0 rank tensors. This is the way all 0 rank tensors must transform when you change coordinate systems--they must be invariant.
Now, back to the point that there are other types of vectors
which do not transform as discussed earlier. Let's take the function
we were just discussing, f(x,y), at some point and ask "how does it
change with small changes in x?" If the function changes by an
amount df when we move to another x location a distance dx away,
then we can write the expression ![]() to tell how f
changes with x. We can do the same in y and have the expression
to tell how f
changes with x. We can do the same in y and have the expression
![]() . Then we could define a vector (call it G)
which has an x component (
. Then we could define a vector (call it G)
which has an x component (![]() ) equal to
) equal to ![]() at
every point in x and y, while it has a y component (
at
every point in x and y, while it has a y component (![]() ) equal
to
) equal
to ![]() at every point. Now, what if we do this same
procedure in the x'-y' coordinate system. First, we need to
convert f into a function f'. We do this such that if a point in
our space has coordinates (x,y) in one coordinate system while the
same physical point has coordiantes (x',y') in the other coordinate
system, then we want f(x,y) = f'(x',y'). That way f' is the
proper representation of f in the primed coordinate system. Now we
again find a vector, G, and we will end up with the x' and y'
components of the G vector such that
at every point. Now, what if we do this same
procedure in the x'-y' coordinate system. First, we need to
convert f into a function f'. We do this such that if a point in
our space has coordinates (x,y) in one coordinate system while the
same physical point has coordiantes (x',y') in the other coordinate
system, then we want f(x,y) = f'(x',y'). That way f' is the
proper representation of f in the primed coordinate system. Now we
again find a vector, G, and we will end up with the x' and y'
components of the G vector such that ![]() and
and ![]() .
.
We now want to figure out how to transform G from one frame to
another. First, we will look at ![]() which says that
which says that ![]() comes from knowing how f'
changes with respect to x' (i.e.
comes from knowing how f'
changes with respect to x' (i.e. ![]() ). To
transform this component of G, we must know how to find
). To
transform this component of G, we must know how to find
![]() using
using ![]() and
and ![]() . This means we will
be using information about how f changes with respect to x and y
(i.e., using
. This means we will
be using information about how f changes with respect to x and y
(i.e., using ![]() and
and ![]() ). We
will also need to use information about how x and y change with
respect to x'. Without taking the time to fully explain the
calculus involved, perhaps the following equation will not be too
surprising:
). We
will also need to use information about how x and y change with
respect to x'. Without taking the time to fully explain the
calculus involved, perhaps the following equation will not be too
surprising:
(Eq 5:6)
Conceptually (though mathematicians would cringe a bit at this
explanation) one can imagine canceling out the dx in
![]() and canceling out the
dy in
and canceling out the
dy in ![]() to see that in
both parts of that equation we are looking at information about
to see that in
both parts of that equation we are looking at information about
![]() . In the first case, we are looking at how
f' changes with respect to x' by way of how x changes with
respect to x', while in the second case we are looking at how f'
changes with respect to x' by way of how y changes with respect to
x'. Adding these two components together as we do in the above
equation gives us a full picture of how f' changes with respect to
x' given information about how f' changes with respect to x and
y.
. In the first case, we are looking at how
f' changes with respect to x' by way of how x changes with
respect to x', while in the second case we are looking at how f'
changes with respect to x' by way of how y changes with respect to
x'. Adding these two components together as we do in the above
equation gives us a full picture of how f' changes with respect to
x' given information about how f' changes with respect to x and
y.
We further note that f' and f are actually the same physical
function, we just use the prime to indicate which coordinate system we
are primarily thinking of. Thus f and f' will both change in the
same way with respect to changes in x and y
(i.e. ![]() and
and
![]() . We therefore rewrite
Equation 5:6 as
. We therefore rewrite
Equation 5:6 as
(Eq 5:7)
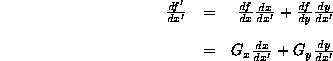
Note that we have substituted ![]() and
and
![]() . The above equation provides the
transformation of
. The above equation provides the
transformation of ![]() given the components of G in the
(x,y) coordinate system. Similarly, we can also find the
transformation of
given the components of G in the
(x,y) coordinate system. Similarly, we can also find the
transformation of ![]() . In the end, simply because of the
way this vector is defined, it transforms as follows:
. In the end, simply because of the
way this vector is defined, it transforms as follows:
(Eq 5:8)
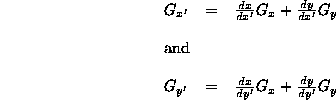
As before, we can rewrite these two equations as follows:
(Eq 5:9)
Note that we are using ratios like ![]() rather than
rather than ![]() (which we used earlier). That means that this is a different type of vector (because it transforms in a different way). The vector we discussed earlier (V) is called a contravariant vector, and the fact that it transforms as shown in
Equation 5:5
is what defines it as that type of vector. The G vector is called a covariant vector, and it is defined as such because it transforms as shown in
Equation 5:9. Usually, we express which type of vector we have by the way we denote its components. For contravariant vectors, we denote their components by putting their indexes (the x or the y) in superscripts:
(which we used earlier). That means that this is a different type of vector (because it transforms in a different way). The vector we discussed earlier (V) is called a contravariant vector, and the fact that it transforms as shown in
Equation 5:5
is what defines it as that type of vector. The G vector is called a covariant vector, and it is defined as such because it transforms as shown in
Equation 5:9. Usually, we express which type of vector we have by the way we denote its components. For contravariant vectors, we denote their components by putting their indexes (the x or the y) in superscripts:
![]() and
and ![]()
While we denote the components of covariant vectors by putting their indices in subscripts:
![]() and
and ![]()
With this notation, the two different transformations begin to take on an easy to remember form. See if you can figure out how the "upper" indices and the "lower" indices match up on both sides of the two transformation equations when they are written as follows:
(Eq 5:10)
and
(Eq 5:11)
Notice that the superscript (or subscript) on one side remains "upper" (or "lower") in the ratio on the other side. Also, note that the summation is always over the index which is repeated on the right side, once in an "upper" position and once in a "lower" position. This basic "formula" helps to produce equations for all transformation in tensor analyses (note this in the next part of this section).
It is interesting to note that in the normal spatial coordinates we are used to using (Cartesian coordinates), ![]() , and there is no distinction between covariant and contravariant vectors. However, in other systems, the difference is there and must be considered.
, and there is no distinction between covariant and contravariant vectors. However, in other systems, the difference is there and must be considered.
Further, we note that with higher rank tensors, they are also defined by the way they transform from one coordinate system to another. For example, consider a second rank tensor, U. It could be that both of its indices are associated with the contravariant type of transformation (note: the following actually denotes four equations because a'b' can be set to x'x', x'y', y'x', or y'y'):
(Eq 5:12)
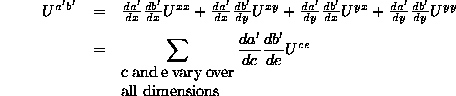
Or they could both be associated with the covariant type of transformation:
(Eq 5:13)
Or it could be a mix of the two:
(Eq 5:14)
Finally, we will see in the next section that any contravariant tensor also has a covariant form (and vice-versa), and we can transform from one form to the other if we know the geometry of the manifold on which the tensors are defined.
And that about ends our introduction to tensors. To sum up, they are geometric entities which have components denoted by some number of indices. Each index can be any of the dimensions in which the tensor is defined, and the number of indices needed to specify a component of a tensor is called the tensor's rank. We are familiar with 0 and 1 rank tensors (numbers--or "scalars"--and vectors). Finally, the way one transforms a tensor from one coordinate system to another depends on the type of tensor, and it (in fact) defines what it actually is to be a tensor. Each index of a tensor will transform in either a contravariant way or a covariant way.
These are the basic ideas behind tensors, and they allow us to define some very powerful mathematics. If you are familiar with the usefulness of vectors, then you have touched the surface of the usefulness of tensors in general. In the following section, we will look at two particular tensors, and we will see that they can be quite useful.
5.7 The Metric Tensor and the Stress-Energy Tensor
Now that we have had a glimpse at tensors, let's consider a couple that will be important to us. The first is called the metric tensor. I mentioned a couple of sections ago that this tensor is related to the invariant interval for a certain coordinate system on a given manifold. So, let's go back and look at a the two specific invariant intervals which we introduced. First, in normal, x-y, Cartesian coordinates, we have Equation 5:1 duplicated here:
(Eq 5:15--Copy of Eq 5:1)
Second, on the surface of a sphere, using the L-H coordinate system which we defined, we have Equation 5:2 duplicated here:
(Eq 5:16--Copy of Eq 5:2)
Now, let's make this more general by considering an arbitrary, two dimensional manifold and an arbitrary coordinate system on that manifold. Let's call the coordinates "a" and "b". Now, in general, the invariant interval on this manifold is defined in terms of the square of that interval ![]() . The equation for
. The equation for ![]() involves the infinitesimal distances da and db in second order combinations. By second order combinations, I mean, for example,
involves the infinitesimal distances da and db in second order combinations. By second order combinations, I mean, for example, ![]() or
or ![]() . Thus, in general, the invariant interval will have the following form (note: the g components are generally formulas of "a" and "b"):
. Thus, in general, the invariant interval will have the following form (note: the g components are generally formulas of "a" and "b"):
(Eq 5:17)
In that equation you see the four components of the metric tensor in this two dimensional, a-b coordinate system. They are the "g's" in the equation. For our x-y coordinate system, we have
(Eq 5:18)
For our L-H coordinate system, we have
(Eq 5:19)
So, we can construct the invariant interval if we know the metric tensor for a coordinate system on a manifold. Now, remember that we said that the form of the invariant interval for a particular coordinate system tells us everything there is to know about the manifold for which those coordinates are valid. So, now we see that all we need to know is the form of the metric tensor. Once we know g, we know the geometry of the manifold. Using tensor analysis, we can take the metric tensor and find an equation for geodesics on the manifold. We can use it to find out all about the curvature of the manifold. We can even use it to find the dot product (we will discuss this a bit later) of two vectors in a particular coordinate system.
Another thing the metric allows us to do is something generally called "raising" or "lowering" indices. Basically, if you consider a tensor with a contravariant index (which transforms in a particular way as discussed earlier), then there is another way to express the tensor as one which has a covariant index (and vice versa). That is to say that the geometric entity represented by the tensor with the contravariant index has another representation which involves a covariant index. For example, consider the tensor ![]() , which has a contravariant index, a. There is a corresponding covariant tensor,
, which has a contravariant index, a. There is a corresponding covariant tensor, ![]() , which can be found using the metric of the space (and coordinate system) we are dealing with. Here is an example of how you find it (finding
, which can be found using the metric of the space (and coordinate system) we are dealing with. Here is an example of how you find it (finding ![]() when you know
when you know ![]() ) for a coordinate system with some arbitrary coordinates, x and y:
) for a coordinate system with some arbitrary coordinates, x and y:
(Eq 5:20)
For a general space and coordinate system, you can write this rule as follows (remember, "a" can be any one dimension in the space, so this represents a number of equations):
(Eq 5:21)
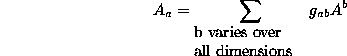
Similarly, if you know the covariant form of A (![]() ) you can find the contravariant form by using the following:
) you can find the contravariant form by using the following:
(Eq 5:22)
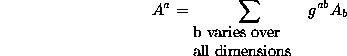
But that equation involves the contravariant form of the metric ![]() . In the invariant interval, the metric is expressed in its covariant form
. In the invariant interval, the metric is expressed in its covariant form ![]() . It is therefore important for the reader to remember as we discuss various metrics below, that for all of them we have
. It is therefore important for the reader to remember as we discuss various metrics below, that for all of them we have
(Eq 5:23)
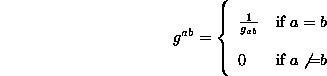
Thus, using the metric tensor, one can "raise" or "lower" any index of a tensor. Remember, what one is really doing is finding a form of that tensor which transforms in a different way.
With this example of how the metric can be used, we will end our discussion of this tensor. To sum up, the metric tensor on a manifold is a very important entity which not only tells us all about the manifold's geometry, but which also provides a very powerful tool which allows us to deal with that geometry mathematically.
The second tensor we want to mention is the stress-energy tensor. I don't want to get too deep into a discussion of the stress-energy tensor, but the reader should know a couple of key points. With the stress-energy tensor, we see our first example of a tensor explicitly defined in four dimensional space-time (though later we will look at the metric tensor defined in 4-d space-time). The stress-energy tensor (T) is also a tensor of rank 2 (like the metric tensor), which gives it 16 components in 4 dimensions. Sometimes we express such a tensor in the form of a matrix as follows:
(Eq 5:24)
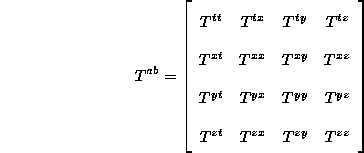
There you can see the 16 different components. Now, each of these components tell us something about the distribution and "flow" of energy and momentum in a region. More precisely, T contains information about all the stresses and pressures and momenta in a region. For example, The "tt" component of the stress-energy tensor would be the density of the energy in the region (the amount of energy--including mass energy--per unit volume).
As to why the stress-energy tensor is important to us, that will be discussed further in a bit. However, here we can note the following in order to pull us back towards our discussion of relativity and gravity: In Newtonian physics, gravity was caused by the density of mass in an area. However, in SR we find that mass is just a form of energy, and so we might think that the "tt" component of the stress-energy tensor would be the right thing to look at when it comes to gravity. However, if we write a rule using one component of a tensor, then because the value of that component will depend on your coordinate system (or frame of reference in space-time) then the rule will also be frame-dependent. In short gravity would not be an invariant theory, and it would require a preferred frame if we based it only on the "tt" component of T. However, if we use all the components of a tensor to form our theory, then (as it turns out) the theory can be made frame-independent. Einstein thus considered the possibility that the whole stress-energy tensor would need to play a part as the source of gravity. Add to this some insight on curved manifolds and you end up with general relativity, as we will see.
5.8 Applying these Concepts to Gravity
Now that we have discussed manifolds and their properties along with some of the basic concepts of tensors, let's see how all of this applies to relativity and gravitation. First, I will go over the main ideas which lead us from what we have discussed so far to a general relativistic theory. After that, I want to mention a few notes on the physics and the mathematics we will be using given the concepts we have gone over. Next, we will go back and look again at special relativity while applying a bit of our new knowledge. This will show that GR is indeed general, because when applied to space-time without the presence of gravity it will explain a special case--special relativity. Finally, we will look quickly at a specific application of the GR concepts to a space-time in which there is a gravitational field. This application will focus on a particular class of stars and black holes.
Let's get started with the basic ideas which combine the concepts we have discussed to produce GR. Here I will simply state the main ideas without an explanation of their application. You will get some feel for their application in our two examples to follow.
So, here are the main claims of GR which involve the concepts we have discussed. First, the space-time in which we live is a four dimensional manifold. On that manifold there is a metric tensor (or just "a metric") which describes the geometry of space-time. The metric can be used to find geodesics on the space-time manifold, and when an object (only being acted on by gravity) goes from one point in space-time to another point in space-time (note: these are not just two points in space, but two points--i.e. events--in space-time), it moves between the points by following a space-time geodesic. Therefore, all the information necessary for us to determine how such objects move through space-time is held within the form of the metric. How, then, do we determine the metric? Well, the metric of space-time in a region is itself determined (in a not-too-trivial way) from the stress-energy tensor (T) which is affecting the region. This then is the new theory of gravity which relativity has produced. The stresses and pressures and momenta in a nearby region produces a stress-energy tensor which, in turn, changes the metric of the nearby space-time (making its geometry "curved"). This forces objects in the region to follow specific paths (geodesics) through the "curved" space-time, and we attribute this motion to gravitational effects.
As a conceptual example, consider a football being thrown from the surface of the earth. Because of the mass of the earth, the space-time the football is traveling through is a curved manifold, and the football follows a "straight line" geodesic in the four dimensional curved space-time. To us, the football's path is curved through three-space, but if we could somehow experience the time dimension as a spacial dimension (i.e. if we were four dimensional beings) and if we followed the path of the football in the four-space, we would seem to be following a straight line on our four dimensional curved manifold. However, in reality, the fourth dimension of time does not act like the other dimensions in our perception of the space-time manifold. Thus we do not see the actual four dimensional path of the football, we only see the path in three dimensions while the fourth component of the path is revealed to us as a dynamic component of the ball's motion through time. That's why we can't see that its path is a "straight line" in curved space-time. The stright-line is revealed to us as curved motion, and we attribute that motion to gravitational effects.
5.8.2 Some Notes on the Physics and the Math
Before we go on to our two examples, I wanted to mention a couple of points about the mathematics which can be used to develop physics in a particular space-time.
First, note that for any space-time there is a four dimensional metric involved. This metric can be used to find the invariant interval between two space-time points. That interval (recall) can generally be expressed as
(Eq 5:25)
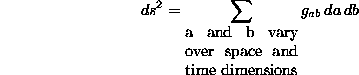
Second, consider a vector in our four dimensional space. Such a vector (usually called a four-vector) has four components, three relating to space and one relating to time. Now, in general, the values for these components will depend on the coordinate system/frame of reference in which you are considering the vector. However, we can use the metric to act on two four-vectors to produce an invariant number. In other words, if there are two four-vectors in a space-time, then two different observers using two different frames of reference will each find different x, y, z, and t coordinates which represent those two vectors in their respective frames. However, when they each act on those two vectors in a specific way using their own coordinate systems and using their own representation of the metric, they will each produce the same particular number. The action on the two vectors is called the dot product of the vectors, and many of you may have heard of and used it before (though perhaps you didn't realize you were using the metric--if you have ever had to remember how to produce a dot product in polar coordinates, then you have seen how the metric in that coordinate system affects the way you produce the dot product).
So, consider two four vectors, U and V. Remember that these are simply tensors with either contravariant or covariant components. Now, we can produce the dot product of U with V as follows.
(Eq 5:26)
This produces a frame invariant number (a scalar), and if U and V have particular physical properties in space-time, then we can use the dot product to produce frame invariant physical rules in a particular space-time.
For our third note in this section, let's discuss the time between two events. It will be useful for us to find a frame-independent way of expressing that time. To explore this a bit, consider an observer who is not being acted on by any forces other than gravity. Because of gravity, he will simply follow a geodesic through space-time--being at certain points in space at particular times. Now, consider two events which each occur at the position of our observer, but which occur at two different times on our observer's clock. For such events, the time on the observer's clock which ticks off between the two events is called the "proper time" (T, though it is usually denoted using the Greek letter "tau") between those two events. The time this observer reads on his clock does not depend on what any other observer sees or does, and T is therefore a frame-invariant way of specifying a time between two such events. Of course, the time as measured in other frames will be different from T, but every frame will agree that for the one, unique observer who naturally follows space-time curvature to be at the position of both events, T is the proper time which he measures on his clock.
We should note that not all events can be connected by the natural space-time path of an observer because no observer can travel faster than light in that space-time. Any two events which can be connected by an observer's natural space-time path are called "time-like separated", and T can easily be defined for such events.
Now, consider the invariant interval for some observer's space-time path between two particular points. Remember that in general the invariant interval is a function of your position in space-time. Thus, as soon as you start moving down a path, the invariant interval begins to change. We discussed this fact briefly in Section 5.5 and decided that we would deal with it by breaking up the path into small bits and consider the invariant interval at each bit. Therefore, rather than discuss the entire interval between the two events, it is better to consider just one point along our observer's path and look the infinitesimal (ds) at that point. That infinitesimal in four dimensional space-time is generally made up of an infinitesimal change in space and an infinitesimal change in time. However, remember that for the observer and the two events we are considering, both of the events occur right at the observer's position. So, for him there is no spatial distance (dx' = 0, dy' = 0, and dz' = 0) between any two points on the path. Therefore, the invariant interval at any point on his path as calculated using his coordinates must be made up of only changes in his time coordinate (dt'). Thus, the value of the invariant interval at some point on the observer's path is given totally by the infinitesimal change in the proper time (dT = dt', the infinitesimal change in time on our observer's watch). We can therefore write the following (taking the spatial components out of Equation 5:25 ):
(Eq 5:27)
Notice that the component of the metric tensor in the above equation is expressed in the coordinates of the observer we are considering (i.e. we are specifically using t' and not t). This must be the case, because it is only when we measure the infinitesimal invariant interval (ds) using his coordinates that we can disregard any spatial component and write the interval totally in terms of dT. However, since this observer is free falling (only being acted on by gravity), then
recall
that his local space-time is flat, regardless of the global geometry of the space-time he is in. Thus, for small distances in space and time in his coordinate system (i.e. for infinitesimals like dt') his space-time can be considered to be that of special relativity (flat space-time). We will find out in the next section what ![]() is for the flat space-time of SR, and when we plug this into
Equation 5:27
we will find that
is for the flat space-time of SR, and when we plug this into
Equation 5:27
we will find that
(Eq 5:28)
That equation is true for any space-time, because the space-time of the observer is locally flat regardless of the global geometry of the space-time we are considering.
So, how will this help us with the physics? Well, specifically, this gives us a way to define the momentum of an object in any space-time. Consider a free-falling object of mass m. In some coordinate system, the object's position in one coordinate (say "a") can be changing. Note that "a" could be x in an x-y-z coordinate system, r in polar coordinates (which we will discuss later), etc. Now, as the object changes spatial coordinates in this system, it will follow a natural geodesic path through space-time. As the object's position in "a" changes by some infinitesimal amount (da) its own "clock" will tick off some small time (dT--note that this is a proper time because it is measured on the clock of the object itself). In that case, the "a" component of the momentum for that object in this coordinate system will be expressed as
(Eq 5:29)
Notice that if we consider the situation where "a" is the time coordinate itself in our system, then we have a sort of "temporal momentum" who's significance will be discussed in the next section. Thus, ![]() actually has four dimensions, and is, in fact, a four-vector. Combine this with our discussion of four-vectors above, and we will find some useful physics, as we will see in the following examples.
actually has four dimensions, and is, in fact, a four-vector. Combine this with our discussion of four-vectors above, and we will find some useful physics, as we will see in the following examples.
5.8.3 First Example: Back to SR
The most simple application of the ideas expressed in Section 5.8.2 is one which we have already looked at (though without using the concepts discussed in that section). It is the situation where there is no gravitational field. That is exactly the situation we were considering when we discussed special relativity. In special relativity, there is no gravitational field. All the components of the stress-energy tensor are identically zero.
Now, we will figure out the metric of space-time in such a case by examining what we already know about special relativity. So, let's go back to our space-time diagrams. (By the way, our diagrams only considered one of the spatial dimensions, but we will incorporate the other two in this section.) Consider two observers who start out moving parallel to one another on the diagram. This would mean that they start out with the same velocity in any inertial frame. Well, in special relativity (with no gravitational field) the two observers will continue to remain on parallel paths on the space-time diagram. This is the property of a flat manifold, so in SR, space-time is "flat".
Before we go on, it will be helpful for us to redefine the time variable in our space-time coordinates. Instead of "t", consider the combination "c t" (where c is the speed of light). For convenience, we will simply define a new variable, w, where
(Eq 5:30)
Then we can use w in place of t in our coordinates. This is actually a fairly natural substitution in a couple of ways: First, note that w has the units of length, just like x, y, and z do. Second, using w on our space-time diagrams makes them a little more general. Why? Well, remember how we defined the units of length and time to be the light-second and the second? We did this so that a light ray would make a line at a 45 degree angle on our diagram. Well, with a w-x coordinate system, this will automatically be the case, regardless of what units you use. To see this, note that the value of t at a certain value of w is just the time it takes for light to travel that length, w (because t = w/c). For example, the point x = 1 light-second and t = 1 second corresponds to the point x = 1 light-second and w = 1 light-second. So, on both an x-t diagram and on an x-w diagram, a light beam would make a 45 degree angle with the x axis by going through the point (1,1). However, if we wanted to, we could now use a meter as our unit of length. Then, when w = 1 meter, t would just be the time it takes for light to travel 1 meter. So, the point x = 1 meter, w = 1 meter also lies on the light path, and again, that light path would automatically make a 45 degree angle with the x axis by going through the point (1,1). For consistency, we will continue to use units of seconds and light-seconds, but we will now use "w" in units of light-seconds to indicate time in our discussions and diagram (remember, the length "w" just represents the time it takes light to travel that length).
Now, let's look at a change in coordinates on the flat space-time of SR. In space-time, a change in coordinates can represent a change in an observer's frame of reference. So, when we discussed two observers who were moving with respect to one another, we were looking at two different coordinate systems (x-t and x'-t', or now, x-w and x'-w') which both correctly described space-time in SR. This leads us to consider the invariant interval, because we know it must be the same for each of these two coordinate systems. So, let's take a closer look at these coordinate systems on our diagrams and see if we can't define the invariant interval (which, remember, is just another way of writing the metric).
We will specifically want to consider infinitesimal lengths like
dx. So, let's look at a small line segment which lies on a
particular geodesic--a geodesic we know a little about. That geodesic
is the path which light follows. Like anything else being acted on
only by gravity, light must follow a geodesic on the space-time
manifold. So, for the particular case of a light path, a small segment
on that path would have an x component (dx) and a t component
(dt); however, we now want to begin thinking of w as the unit which
represents time, so we note that a small change in t (dt)
represents a change in w of ![]() . Now, since the
small distance light travels (dx) divided by the time (dt) it took
it to travel that distance is defined as the speed of light, then we
have the following:
. Now, since the
small distance light travels (dx) divided by the time (dt) it took
it to travel that distance is defined as the speed of light, then we
have the following:
(Eq 5:31)
which can be rewritten as
(Eq 5:32)
That means that dx = dw (for light). Now, since we always define the invariant interval in terms of the infinitesimal lengths squared, we will actually want to square both sides of that equation and then bring everything to one side so as to get the following:
(Eq 5:33)
Now, because the speed of light is the same for all inertial observers, the above equation must be true for all frames of reference. Thus, we might consider the idea that the invariant interval for any small line segment (not just for light) is given in SR by
(Eq 5:34)
and this turns out to be the case. The light path, then, is just the case where ![]() .
.
Now, let's note a few things about this interval. First, it is independent of where you are in space-time. All that matters is the lengths dx and dw, regardless of what actual x and w position you have. This means that the distances (like dx) don't have to be infinitesimal, because the equation remains true regardless of how far you extend dx and dw. Thus, let's consider the case where one side of the line segment is at x = w = 0 (the origin). Then dx will be the x distance from the origin to the end of the line segment (which in this case can be as far away as we like), and dw will be the w distance to that point. In other words, for SR, dx and dw can be replaced with x and w when we consider one side of the line segment to be at the origin. Further, consider a point in space-time with coordinates (x,w) in the o observer's coordinates and (x',w') in the o' observer's coordinates. Since the value of the invariant interval is the same for any frame of reference, the following must be true:
(Eq 5:35)
Let's see that this is the case on our space-time diagrams. Diagram 5-9 shows a space-time diagram with two coordinate systems indicated, one for an observer o, and a second for an observer (o') moving with velocity 0.6 c with respect to o. (Note that now we use w = ct for the time axes.) There is also a point marked "*" on the diagram. The x'-w' coordinates for that point are clearly shown to be x'= 1 light-second and w'= 2 light-seconds (i.e. t'= 2 second, remember?). The x-w coordinates are x = 2.75 light-seconds and w = 3.25 light-seconds.
|
|
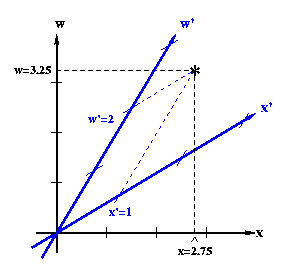
|
We therefore find the following:
(Eq 5:36)
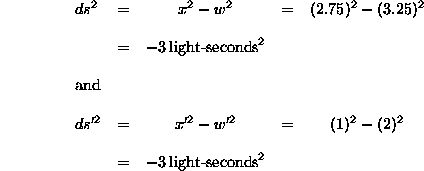
There are a couple notes to make about this outcome. First, of course, we note that ![]() , as it must be. In fact, it is the form of the invariant interval and the fact that it must be invariant from one coordinate system to another that causes the transformation from x-w to x'-w' to look as it does. If the x' and w' axes didn't look the way they do relative to the x and w axes in our diagrams, then the interval would not be invariant. Note that if the "-" sign in the invariant interval were a "+" sign, then the invariant interval would look just like the one for a normal, space-only x-y coordinate system where
, as it must be. In fact, it is the form of the invariant interval and the fact that it must be invariant from one coordinate system to another that causes the transformation from x-w to x'-w' to look as it does. If the x' and w' axes didn't look the way they do relative to the x and w axes in our diagrams, then the interval would not be invariant. Note that if the "-" sign in the invariant interval were a "+" sign, then the invariant interval would look just like the one for a normal, space-only x-y coordinate system where ![]() . Then, the coordinate transformation to x'-w' would be just like a rotation of coordinates (see
Diagram 5-10
). The "-" sign in the SR interval causes one of the axes to rotate in the opposite direction from the other when we do our space-time coordinate transformation.
. Then, the coordinate transformation to x'-w' would be just like a rotation of coordinates (see
Diagram 5-10
). The "-" sign in the SR interval causes one of the axes to rotate in the opposite direction from the other when we do our space-time coordinate transformation.
Second, note that the interval squared is, in fact, negative. This is not too distressing, because we know that physical lengths on our diagram do not represent the space-time "lengths" which the invariant interval gives us. If they did, then the invariant interval for special relativity would be just like the x-y form of the invariant interval (since the physical lengths on our diagrams are just normal lengths on the flat paper/screen we draw them on). Now, the actual length of an infinitesimal interval on a manifold is usually defined to be the square root of the absolute value of ![]() . Thus, we can still make sense of lengths, even when the invariant interval squared is negative.
. Thus, we can still make sense of lengths, even when the invariant interval squared is negative.
|
|
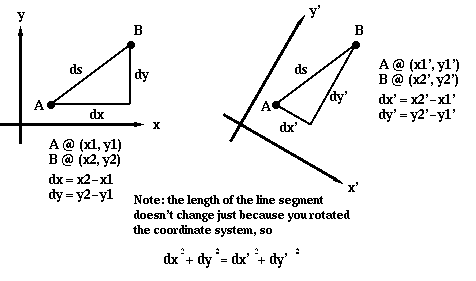
|
The reader may have noted that thus far in our look back at special relativity we have still only included two of the four dimensions of space-time. The other two (y and z) could actually replace x in any of our discussions, and so they play the same roll in the invariant interval as x does. Therefore, the total four dimensional invariant interval for special relativity is given by
(Eq 5:37)
Finally, let's talk about some physics in this space-time using the concepts discussed in the previous section. First, consider the proper time between two time-like separated events. Recall that we defined this time such that:
(Eq 5:38)
We now know that ![]() for SR from the above, so
for SR from the above, so ![]() for SR. This is how we got
Equation 5:28
, which is duplicated here:
for SR. This is how we got
Equation 5:28
, which is duplicated here:
(Eq 5:39--Copy of Eq 5:28)
in the previous section. However, since we are now working with w for our time coordinate, we should define dW = c dT, and rewrite Equation 5:39 as
(Eq 5:40)
Now, let's consider the observer which followed the t' axes in Diagram 5-9 such that his velocity was 0.6 c. Consider the O observer's frame of reference, and note that if it takes O' a certain time (dw) to travel a certain distance (dx) in the O observer's coordinates, then it must be the case that dx/dt = 0.6 c. So dx/dw = 0.6, or
(Eq 5:41)
This, then, is true all along the w' axes (the line that O' follows through the O observer's coordinate system). So, the invariant interval (considering only two dimensions once again) at any point along the w' axes must be given by the following (using Equation 5:37 with only x and w coordinates and substituting Equation 5:41 ):
(Eq 5:42)
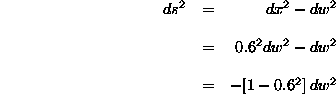
plugging this into Equation 5:40 we find that
(Eq 5:43)
so,
(Eq 5:44)
Since dW just represents an infinitesimal time as measured on our "moving" observer's clock, and dw an infinitesimal time measured on our clock, Equation 5:44 is just the equation which shows time-dilation effects in SR, and it was quickly derived using our new knowledge.
For another physics consideration, look at the momentum four-vector. We defined this earlier ( Equation 5:29 ) and it is duplicated here:
(Eq 5:45--Copy of Eq 5:29)
Again, we want to use dW = c dT, and we thus find
(Eq 5:46)
For us, we consider the situation where "a" is the x dimension. Then, ![]() for the "moving" observer himself is zero (because all along the w' axes we have dx' = 0 by definition, i.e. he is not moving relative to himself). However, for the O observer (for whom the "moving" observer moves a distance dx in a time dw) we find the following from
Equation 5:46
by substituting x for a(Note that from
Equation 5:44
we can write
for the "moving" observer himself is zero (because all along the w' axes we have dx' = 0 by definition, i.e. he is not moving relative to himself). However, for the O observer (for whom the "moving" observer moves a distance dx in a time dw) we find the following from
Equation 5:46
by substituting x for a(Note that from
Equation 5:44
we can write ![]() , and we are substituting that here. We also use dw = c dt and v = dx/dt in this equation.):
, and we are substituting that here. We also use dw = c dt and v = dx/dt in this equation.):
(Eq 5:47)

This is exactly the definition of the momentum we saw in our discussions of special relativity.
However, now we can also look at the time component of the momentum four-vector and figure out what it represents. Again we use Equation 5:46 , but here we substitute w for x:
(Eq 5:48)
But this is just the energy we had defined in SR (![]() ) divided by c:
) divided by c:
(Eq 5:49)
And so, we now know all about the components of the momentum four-vector of a particle: three are the spatial components of the momentum of the particle, and the time component represents the energy of the particle divided by c.
As a final bit of physics, consider the dot product (as defined in Equation 5:26 ) of the momentum four-vector with itself:
(Eq 5:50)
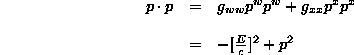
(Note that the total momentum of this observer is ![]() , and so we write
, and so we write ![]() in the last line to mean the total momentum squared). Now, recall that the dot product is invariant, so that if any observer measures the energy and momentum of a particle and calculates the above equation in his frame of reference, he must find the same number that any other observer would find in any other frame of reference. This shouldn't come as too much of a surprise if we look back for a moment. Back when we discussed energy and momentum in special relativity, we found in
Equation 1:7
that
in the last line to mean the total momentum squared). Now, recall that the dot product is invariant, so that if any observer measures the energy and momentum of a particle and calculates the above equation in his frame of reference, he must find the same number that any other observer would find in any other frame of reference. This shouldn't come as too much of a surprise if we look back for a moment. Back when we discussed energy and momentum in special relativity, we found in
Equation 1:7
that ![]() . Thus, we find that the dot product in
Equation 5:50
is simply equal to
. Thus, we find that the dot product in
Equation 5:50
is simply equal to ![]() . Since m and c are invariant (remember, m is the rest mass), we could have already known that the formula in
Equation 5:50
would be invariant.
. Since m and c are invariant (remember, m is the rest mass), we could have already known that the formula in
Equation 5:50
would be invariant.
We have therefore been able to find all the major physics equations we saw in special relativity by simply apply some tensor analyses using the metric of flat space-time.
So, to sum up, we have found the following: For SR, where there is no gravitational field, space-time has the properties of a flat manifold. The invariant interval of a flat space-time manifold is given by the following:
(Eq 5:51--Copy of Eq 5:37)
That interval tells us all about the nature of space-time in SR. The fact that the contribution of the time component (dw) is negative where as the spatial components have positive contributions is what gives the coordinate transformation between different frames of reference its unique form. Thus, it is the negative sign which essentially causes time dilation and length contraction effects, and it is the fact that the speed of light is invariant which causes that sign to be negative.
5.8.4 Second Example: Stars and Black Holes
In this second example, we will briefly look at the description GR gives us for the gravitational field of certain stars. We will also take a look at one of the most widely publicized consequences of GR--black holes.
To make our discussion simpler, the types of stars we will be considering will be spherically symmetric. What does that mean? Well, consider an imaginary sphere with some radius. Place the center of that sphere at the center of the star. If the star is spherically symmetric, then the strength of the gravitational field everywhere on the surface of our imaginary sphere will be exactly the same. For example, a star who's density is spherically symmetric and which is not spinning would work.
Now, it will be helpful for us to discuss the space around the star in terms of spherical coordinates; therefore, I should make sure the reader knows what these coordinates are. Rather than using x, y, and z coordinates for the three dimensional space around the star, we will use r, a, and b coordinates, which I will define here. In Diagram 5-11 I have tried to draw (in three dimensions) an z-y-z coordinate system, and I have marked a point in space, *. There is a line segment drawn from the origin (o) to that point, and the lengths of the x, y, and z components of the line segment are the values for the x, y, and z coordinates of the point, *. These components have been indicated on the diagram using "dotted" lines. Now, note that there is one other dotted line which is not labeled. If you imagine a light shining down on our line segment, then the unlabeled dotted line would be the shadow that light produced on the x-y plane. It is called the projection of the line segment on the x-y plane, but let's just call it "the x-y component" for convenience.
|
|
|
Now we can define the r-a-b coordinates for the point, *. First, the distance from the origin to the point (the length of the line segment) is the "r" coordinate as indicated on the diagram. Next, the angle between the z axes and the line segment is our "a" coordinate (though it is usually denoted by the Greek letter "theta" (![]() )). It too is indicated on the diagram. Finally, there is the angle between x and the x-y component of the line segment. That angle is our "b" coordinate (though it is usually denoted by the Greek letter "phi" (
)). It too is indicated on the diagram. Finally, there is the angle between x and the x-y component of the line segment. That angle is our "b" coordinate (though it is usually denoted by the Greek letter "phi" (![]() )), and it is indicated on the diagram as well. Thus, with r-a-b coordinates as defined here, we can specify any point in three dimensional space.
)), and it is indicated on the diagram as well. Thus, with r-a-b coordinates as defined here, we can specify any point in three dimensional space.
As a final note about this coordinate system, we should look at the metric of a flat 3-space using these coordinates. For an x-y-z system, the metric is (of course) given by this invariant interval:
(Eq 5:52)
However, for our new coordinate system in the same flat 3-space, it is given by the following:
(Eq 5:53)
For convenience, a new infinitesimal (call it du) is sometimes defined such that:
(Eq 5:54)
Then we can rewrite Equation 5:53 as
(Eq 5:55)
We will therefore continue to use du throughout this discussion, but remember it is just a convenient way to write the a and b components of the invariant interval.
Next, let's look at some properties of the star we will be considering. Basically, we will say it has a total mass of m(star) and a radius R. The center of the star will be centered at the origin, o. Finally, we will only be considering the gravitational field outside of the star itself. In general, physicists are interested in the gravitational field inside the star as well, but we will not worry about it that much.
We also want to define a new variable for mass using the Newtonian gravitational constant G. In Newtonian gravitation, the force between two objects of mass m1 and m2 which are a distance r apart is given by
(Eq 5:56)
(where ![]() and we note that kg is the symbol for kilogram). We will use G to define a new variable, M, such that
and we note that kg is the symbol for kilogram). We will use G to define a new variable, M, such that
(Eq 5:57)
Notice that M has the units of meters, and so M gives us a way of specifying the mass of an object in units of meters (similar to the way w allows us to specify time in units of meters). It is called the "geometrized" mass. So, using M we can say that an object has a mass of 1 meter, and one can decipher what mass we are talking about in terms of conventional units by using
Equation 5:57. As a note, a mass of M = 1 meter corresponds to m(conventional) ![]() , the mass of the sun is M(sun) = 1477 meters (
, the mass of the sun is M(sun) = 1477 meters (![]() ), and the mass of the earth is M(earth) = 0.004435 meter (
), and the mass of the earth is M(earth) = 0.004435 meter (![]() ).
).
Now, with this information in mind, the next step is to figure out what the metric of the space-time around the star would be because of the stress-energy tensor of the star. Generally, one uses the fact that we are considering spherically symmetric stars in order to make some assumptions about the form of the metric. One then uses this general form to calculate the general form the stress-energy tensor would have. Finally, one uses what we know physically about the star compared to the form of the stress-energy tensor, and one can decipher what equations must have made up the metric in the first place. In the end, one finds a metric for the space-time around this type of star, and for our purposes, we will simply state that end result. Thus, the metric is as follows (expressed in terms of the invariant interval):
(Eq 5:58)
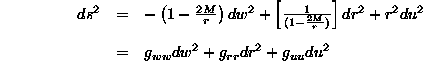
Note that we are using du as defined earlier, and we are using dw = c dt as our time component as discussed in the previous section. Also, we are using M (as defined in Equation 5:57 ) to denote the mass of the star rather than m(star). This metric is known as the Schwarzschild metric.
The next step, then, is to show that we can get useful physics by considering this metric. We will again (as we did with the Special Relativity discussion earlier) be looking at a particle of mass m, and here we will be interested in its motion in the space-time around the star. Because of the spherical symmetry of the space-time, the motion of such a particle will remain within a plane, and we can orient our coordinate system so that the plane is one where the angle "a" = 90 degrees (and sin(a) = 1). Since the particle doesn't move out of that plane, there is never a change in the angle "a" (da = 0). Thus, for this particle, we can consider the metric as follows (putting sin(a) = 1 and da = 0 into Equation 5:58 ):
(Eq 5:59)
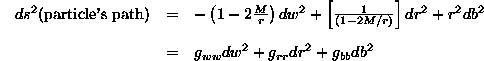
In the interest of time (because we simply haven't been able to cover everything we need to know about tensor analyses in this text), I will have to simply state a couple of facts which we will use to produce the physics we will look at. Namely, we notice that the form of the metric depends on your particular position in r (because ![]() ,
, ![]() , and
, and ![]() are all functions of r). However, none of the metric's components are functions of w. Because of that, as it turns out,
are all functions of r). However, none of the metric's components are functions of w. Because of that, as it turns out, ![]() (the covariant form of the time component of the momentum four-vector) is constant throughout the motion of the particle. The metric is also independent of the angle b. This, as it turns out, implies that
(the covariant form of the time component of the momentum four-vector) is constant throughout the motion of the particle. The metric is also independent of the angle b. This, as it turns out, implies that ![]() is a constant. We can therefore define two constants, E and L such that
is a constant. We can therefore define two constants, E and L such that
(Eq 5:60)
and
(Eq 5:61)
where m is the mass of the particle. These definitions will simplify the equations we will produce below (and they are related to our usual concepts of energy and angular momentum, so the fact that they are constant basically say that energy and angular momentum are conserved as the particle moves).
Now, so far we have only defined the contravariant form of the momentum, ![]() . However, when we discussed the metric tensor we learned how to use it to "raise" and "lower" indices. So, we can write the following from
Equation 5:22
:
. However, when we discussed the metric tensor we learned how to use it to "raise" and "lower" indices. So, we can write the following from
Equation 5:22
:
(Eq 5:62)
Note that we are considering the case where the angle "a" is a constant so that ![]() in
Equation 5:62. Also recall that in
Equation 5:23
we noted how to go from contravariant to covariant forms of the metric. For the metrics we are discussing we thus have (note that the metric components come from
Equation 5:59
).
in
Equation 5:62. Also recall that in
Equation 5:23
we noted how to go from contravariant to covariant forms of the metric. For the metrics we are discussing we thus have (note that the metric components come from
Equation 5:59
).
(Eq 5:63)
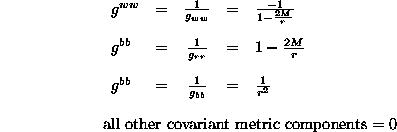
Thus, only the ![]() part remains in
Equation 5:62
giving us the following (note that I substitute using
Equation 5:60
):
part remains in
Equation 5:62
giving us the following (note that I substitute using
Equation 5:60
):
(Eq 5:64)
Similarly we can find the equation for ![]() :
:
(Eq 5:65)
Now, recall that in the last section we found that ![]() was a constant,
was a constant, ![]() . That remains true here, so we find the following:
. That remains true here, so we find the following:
(Eq 5:66)
We can express each of the parts for that equation by substituting in the metric components from
Equation 5:59
, using the above equations for ![]() and
and ![]() , and writing
, and writing ![]() as
as ![]() to get the following:
to get the following:
(Eq 5:67)
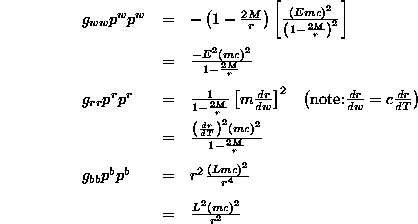
Substitute this into
Equation 5:66
and the ![]() portions will cancel out on both sides giving this:
portions will cancel out on both sides giving this:
(Eq 5:68)
From this, we can find the following equation which describes the orbits the particle can take. It is the equation of motion of the particle:
(Eq 5:69)
Now, it turns out that if one examine this equation for the case of a circular orbit (where r is a constant and dr = 0) and for the case where the mass is small or the orbit is large, we find things to be quite similar to what Newtonian physics predicts. However, it is interesting to note that for orbits for which r can change (elliptical orbits in Newtonian physics) GR predicts something a bit different from Newtonian physics. Basically, in Newtonian physics, the path of the particle in space is a true, closed ellipse. However, with the above equation one finds that the "elliptical" orbit in GR does not close in on itself. Instead, it's as if the ellipse changes position as the particle's orbit goes on. We thus see a difference in the predictions of the two theories, and we will mention this again in the next section.
With this quick look at the physics one can derive using the metric for such a star, we now want to go on and look at a very special case where this metric comes into play. Consider for a moment what would happen if the star's radius were to somehow become smaller than 2 M. Such a thing can theoretically happen for certain stars at the end of their life cycle, (though we won't get into how in our discussion).
So, consider the case where the radius of the star is smaller than 2 M. We can then consider a point above the star for which r < 2 M. Now look back at the metric of the star. If r < 2 M then ![]() becomes positive, while
becomes positive, while ![]() becomes negative. That is to say that the time component of the invariant interval will contribute to the interval in the same way that a space-like coordinate did when r was greater than 2 M, and the radial component will contribute in the same way as a time-like coordinate did when r was greater than 2 M. Further, when r was greater than 2 M, we understood that all particles followed a space-time path which took them "forward" in time. Similarly, when
becomes negative. That is to say that the time component of the invariant interval will contribute to the interval in the same way that a space-like coordinate did when r was greater than 2 M, and the radial component will contribute in the same way as a time-like coordinate did when r was greater than 2 M. Further, when r was greater than 2 M, we understood that all particles followed a space-time path which took them "forward" in time. Similarly, when ![]() becomes negative and
becomes negative and ![]() becomes positive, (when r < 2 M) we find that all particles must continue along a space-time path for which r continually decreases. In other words, the point r = 0 becomes part of the "future" of every particle/observer for which r is less than 2 M. Thus, such a particle will be doomed to fall in toward the center of the star. One can then imagine that the star itself would be doomed to fall in upon itself completely, becoming nothingness at r = 0.
becomes positive, (when r < 2 M) we find that all particles must continue along a space-time path for which r continually decreases. In other words, the point r = 0 becomes part of the "future" of every particle/observer for which r is less than 2 M. Thus, such a particle will be doomed to fall in toward the center of the star. One can then imagine that the star itself would be doomed to fall in upon itself completely, becoming nothingness at r = 0.
This is known as a black hole (specifically, for the metric we are considering, it is a spherically symmetric black hole), and the radius r = 2 M is called the Schwarzschild radius or the event horizon. Any observer with an r coordinate less than 2 M must fall into the point r = 0. Note that at r = 0 our metric becomes truly infinite, and as it turns out, that would be a point where physical laws break down. Such a point is called a singularity. We should also note that any signal (even a light signal) which the observer tries to send outside of the event horizon must also fall into the singularity (because all space-time geodesics for r < 2 M fall into the singularity). Thus, there is no way to get any information from the singularity to the "outside universe". There is no way for one to "see" the singularity and its destruction of physical laws. In that sense, the singularity's existence isn't a problem for our physical laws outside of the event horizon.
As a last consideration about black holes, one might ask what would happen to an observer who starts where his r coordinate is greater than 2 M and then falls toward the event horizon. I won't go through the math, but one finds that in our coordinates, the observer will take an infinite amount of time to reach r = 2 M. However, if we ask about how much time the observer himself reads on his watch as he falls (the proper time) we find that in his coordinates, the time it takes for him to reach the event horizon is finite. To try and understand how this can be, we will start by considering the equation for ![]() (the time component of the momentum four-vector) as defined in
Equation 5:46
:
(the time component of the momentum four-vector) as defined in
Equation 5:46
:
(Eq 5:70)
However, if we look back at Equation 5:64 , we can combine it with Equation 5:70 to find the following:
(Eq 5:71)
Rewriting this, one finds that
(Eq 5:72)
So what does that tell us? Well, consider an observer at the coordinate position r. If a small time ticks in our coordinate w = c t, then the amount of time which ticks on the observer's clock (dW = c dT, where dT is the proper time) depends on the r position of the observer. The smaller his r position (as long as he is above the event horizon) the smaller dW will be for a given dw. This is similar to time dilation in SR, but here it is caused by the gravitational field and not by the relative motion of two observers.
Applying this to our discussion of the observer falling towards the event horizon, we find the following: In our coordinates (w) the clock of the infalling observer (who is constantly falling to smaller and smaller r values) takes longer and longer to tick its next tick. For example, let's say that for the observer's clock, it ticks 10 ticks before it reaches the event horizon. As we mentioned earlier, the coordinate time (w) will have to become infinitely large before the observer will reach the horizon. However, as the observer gets closer and closer to the event horizon, his clock takes longer and longer to tick its next tick. Essentially, in our coordinate system, the observer's clock will never be able to tick the 10th tick. Meanwhile, for the observer, time goes on as usual. For him, therefore, the 10th tick will come, and he will enter the event horizon. However, once in the horizon, he will not be able to send any signals out of the r = 2 M event horizon (in our coordinates). Thus, no one with r greater than 2 M in our coordinates will ever be able to see the infalling observer go into the event horizon. This then explains how we can say that the infalling observer never reaches the horizon according to our coordinate system.
As it was in SR, there are different explanations for how certain outcomes come to be. The explanation depends on what coordinate system you use to explain the occurrences (which means that it depends on your frame of reference). The important point is that the end result of the explanations agree with the each other as far as any physical laws can be applied. In the twin paradox of SR, when the two twins come back together and stand next to one another at the end of the trip, each explanation must agree as to which twin is actually, physically older. For the question of whether an infalling observer reaches the event horizon, regardless of which coordinate system we use, we must agree that the observer is never seen to enter the horizon by any observer outside of the event horizon. The fact that the infalling observer "sees" himself enter the horizon has no physical consequences to the outside world.
Thus, with spherically symmetric stars and black holes, we have found the following: the metric of the surrounding space-time is given by the following (using variables we have defined earlier):
(Eq 5:73--Copy of Eq 5:58)
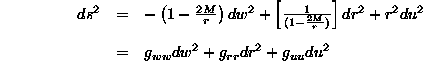
Symmetries in this metric can be used along with the metric itself to find the equations of motion for a particle which moves within this space-time. Finally, the space-time has interesting consequences for the measurement of space and time for observers at different points in the curved space-time surrounding such stars and black holes.
That ends our look at some examples of the application of GR. The only thing left in our discussion of this theory is to show some experimental evidence for its existence, as we will do in the following section.
5.9 Experimental Support for GR
In this section we will take a look at a few experiments which agree with the predictions of GR.
For the first experiment, we use the effect mentioned in the previous section whereby orbits which were supposed to be elliptical according to Newtonian physics didn't actually close in on themselves according to GR predictions. This effect can be seen as a rotation (or precession) of the "long axis" of the elliptical orbit, whereas under Newtonian theory, this axes doesn't move. Now, for the orbits of most planets, this effect is too small to measure. However, for Mercury (which is closest to the sun and would thus be the most affected) the effect is measurable. In fact, measurements taken during the 1800s showed that Mercury's orbit precessed. Now, much of this could be attributed to effects from the gravity of the other planets, however, after all those effects were taken into account, there was still a small amount of precession which wasn't accounted for. The predictions of GR accounted for the left-over difference. It was Einstein who first pointed this out, and this was the first evidence in favor of GR.
For the second experiment we want to consider, note that light, just like anything else being acted on only by gravity, must follow a geodesic in space-time. One can use the metric introduced in the previous section to figure out how light would travel when passing near an approximately spherically symmetric star. What one finds is that the light would be bent by the presence of the star's gravitational field. Now, one might try to make an argument using special relativity by which light with an energy E would be said to have a "relativistic mass" defined by ![]() . One could then figure out how much the light with this "mass" would bend in the presence of a Newtonian-type gravitational field. This, one might hope, could allow the explanation of how light could be bent without considering GR. However, one finds that the amount of bending predicted by this SR-Newtonian method is exactly half as much as the bending predicted by GR. Thus, if we could actually measure the bending of the light, we could figure out which of the two predictions was correct.
. One could then figure out how much the light with this "mass" would bend in the presence of a Newtonian-type gravitational field. This, one might hope, could allow the explanation of how light could be bent without considering GR. However, one finds that the amount of bending predicted by this SR-Newtonian method is exactly half as much as the bending predicted by GR. Thus, if we could actually measure the bending of the light, we could figure out which of the two predictions was correct.
Well, experiments to measure such bending can and have been performed using the sun as the source of gravity and using light from particular stars--light which passes near the sun on its way to us--as the light that gets bent (it was Einstein who suggested this test, by the way). Normally, of course, the sun would be too bright to see stars who's light passes near the sun on its way to us. However, during a solar eclipse, the stars can be seen. When one compares the positions of such stars which one sees during a solar eclipse to the positions where the stars should actually be, one finds that the difference can be attributed to the bending of the light as predicted by GR, while the SR-Newtonian prediction was incorrect by a factor of 2.
The third experiment we will look at involves using highly sensitive atomic clocks taken aboard jets. When one compares the reading on such clocks to clocks which remained on the ground, one finds that the difference (though quite small) can only be accounted for completely if one includes calculations for SR effects and acceleration along with the GR effects of having the jet fly at high altitudes where the gravitational field is not as strong as it is on the surface of the earth.
These are a few examples of experimental evidence that exists in favor of GR. In many cases, more data and more precise measurements would be needed to rule out all theories other than GR; however, all the evidence we do have supports the theory.