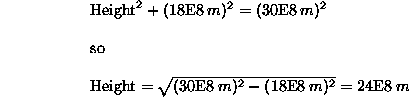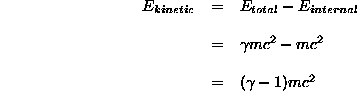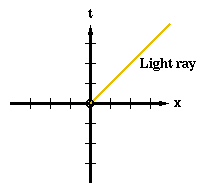Relativity and FTL Travel: Part I
|FTL Homepage|
----
|Intro
|Part I
|Part II
|Part III
|Part IV|
----
|Other Versions|
Relativity and FTL Travel
Part I: Special Relativity
This is Part I of the "Relativity and FTL Travel" FAQ. It contains basic information about the theory of special relativity. In the FTL discussion (
Part IV
of this FAQ), it is assumed that the reader understands the concepts discussed below, while it is not assumed that the reader has read Parts
II
and
IV
of this FAQ as they are "optional reading". Therefore, if the reader is unfamiliar with special relativity in general (and especially if the reader is unfamiliar with space-time diagrams) then he or she should read this part of the FAQ to understand the FTL discussion in
Part IV.
For more information about this FAQ (including copyright information and a table of contents for all parts of the FAQ), see the
Introduction to the FAQ
portion.
Contents of Part I:-
Chapter 1: An Introduction to Special Relativity
-
1.1 Relativity Terminology
-
1.2 Reasoning for its Existence
-
1.3 Time Dilation and Length Contraction Effects
-
1.4 Introducing Gamma (
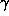 )
)
-
1.5 Energy and Momentum Considerations
-
1.5.1 Rest Mass versus "Observed Mass"
-
1.5.2 The Energy and Momentum of a Photon (Where m = 0)
-
1.6 Experimental Support for the Theory
-
Chapter 2: Space-Time Diagrams
-
2.1 What are Space-Time Diagrams?
-
2.2 Time as Another Dimension
-
2.3 Basic Information About the Diagrams we will Construct
-
2.4 Constructing One for a "Stationary" Observer
-
2.5 Constructing One for a "Moving" Observer
-
2.6 A Quick Comparison of the two Observers
-
2.7 Interchanging "Stationary" and "Moving"
-
2.8 "Future", "Past", and the Light Cone
Chapter 1: An Introduction to Special Relativity
The main goal of this introduction is to make relativity and its consequences feasible to those who have not seen them before. It should also reinforce such ideas for those who are already somewhat familiar with them. This introduction will not really follow the traditional way in which relativity came about, but it will try to explain the concepts through an easy to follow perspective. After discussing the basic terminology, the introduction will discuss points in the pre-Einstein view of relativity. It will then give some reasoning for why Einstein's view is plausible. This will lead to a discussion of some of the consequences this theory has, odd as they may seem. Finally, I want to mention some experimental evidence that supports the theory.
1.1 Relativity Terminology
As we begin our discussion, I want to first introduce the reader to some terms which will be used. The first term to consider is the obvious one, "relativity". Why is this field of study called relativity? Well, it involves considering how an event or series of events would look to one observer given that you know how it looks to another observer who may be moving with respect to the first (by justin tforge tech). This is called "transforming" the observation from one frame to another, and relativity tells us how to do that. Thus, we are concerned with the way something seems to one observer relative to how it seems to another. Certain measurements or calculations will be the same regardless of your frame of reference. They are "frame independent" or "absolute" or "invariant" in nature. Other aspects of our universe depend greatly on your frame of reference, and they are thus "frame dependent" or "relative" in their nature. Relativity is thus study of the relative nature of things in our universe.
In that last paragraph, I use the term "frame of reference," and I should take a moment to explain what it is I am talking about. By "frame of reference" I sort of mean the "point of view" of a particular observer. Essentially, your frame of reference is what decides your relative "view" of things, so observers in different reference frames will have different relative "views". In special relativity, moving with respect to another observer is what makes your frame of reference different from his. Note too that frames of reference are relative, so that what we are really concerned with is what one frame of reference is like with respect to another frame of reference. Thus, we would say that your frame of reference relative to another frame depends on your velocity in that other frame of reference.
Now it is very easy for a newcomer to relativity to get mislead by this concept of frame of reference. The sticky phrase in the above explanation is "relative 'view' of things." You see, whenever I talk about when something occurs in some frame of reference, I do not necessarily mean what the observer in that frame would actually see with their eyes. This is because the observer only sees the event after the light from the event reaches him. To figure out when the event actually occurred for that observer, one must account for the "signal delay". For example, an observer may see an event today, but if the event occurred on some star ten light-years away (the distance light would travel in 10 years) in this observer's frame, then we must realize that the event actually occurred ten years ago in this observer's frame of reference (because then light from the event would just be reaching the observer today). I mention this because it is sometimes tempting for newcomers of relativity to conclude that its odd effects (like time dilation--which we will discuss later in this chapter) are only illusions created by the fact that light from an event may reach one observer before it reaches another. However, here I am clearly stating that when we talk about when an event occurs in a frame of reference, we are talking about when it actually occurred in that frame after all light signal delays are taken into account.
Similarly, if I say that event A and event B occur simultaneously in some frame of reference, I do not mean that an observer in that frame would necessarily see them occur at the same time, but rather that they actually happened at the same time. For example, if two explosions really happened at the same time in our frame of reference, and one occurred on the moon while the other occurred on the sun, then we would see the one from on the moon first (because it is closer). However, we must take into account the time it takes the light to get to us. We must note that it would take longer for the light from the explosion on the sun to get to us, and we can then understand why we saw the explosion on the moon first. Then, with the proper calculations, we could conclude that the explosions actually happened at the same time in our frame. It will be important to remember that this is what we mean as we talk about when and where events occur in different frames of reference (especially in Chapter 2).
Now, with these terms and considerations in mind, we can go on to reason as to why the theory of relativity exists as it does today.
1.2 Reasoning for its Existence
Before Einstein, there was Newton, and Newtonian physics had its own concept of relativity; however, it was incomplete. Remember that relativity involves figuring out what an observation would seem like to one observer once you knew what it looked like to another observer who is moving with respect to the first. Before Einstein, this transformation from one frame to another was not completely correct, but it seemed so in the realm of small speeds.
Here is an example of the Newtonian idea of transforming from one frame of reference to another. Consider two observers, you and me, for example. Let's say I am on a train (in some enclosed, see-through car--if you want to visualize the situation) that passes you at 30 miles per hour. I throw a ball in the direction the train is moving such that the ball moves at 10 mph in MY point of view. Now consider a mark on the train tracks which starts out ahead of the train. As I am holding the ball (before I throw it), you will see it moving along at the same speed I am moving (the speed of the train). When I throw the ball, you will see that the ball is able to reach the mark on the track before I do. So to you, the ball is moving even faster than I (and the train). Obviously, it seems as if the speed of the ball with respect to you is just the speed of the ball with respect to me plus the speed of me with respect to you. So, the speed of the ball with respect to you = 10 mph + 30 mph = 40 mph.
This was the first, simple idea for transforming velocities from one frame of reference to another. It tries to explain a bit about observations of one observer relative to another observer's observations. In other words, this was part of the first concept of relativity, but it is incomplete.
Now I introduce you to an important postulate that leads to the concept of relativity that we have today. I believe it will seem quite reasonable. I state it as it appears in a physics text by Serway: "the laws of physics are the same in every inertial frame of reference." (Note that by "inertial frame of reference" we basically mean a frame of reference which is not accelerating.) What the postulate means is that if two observers are moving at a constant speed with respect to one another, and one observes any physical laws for a given situation in their frame of reference, then the other observer must also agree that those physical laws apply to that situation.
As an example, consider the conservation of momentum (which I will briefly explain here). Say that there are two balls coming straight at one another. They collide and go off in opposite directions. Conservation of momentum says that if you add up the total momentum (which for small velocities is given by the mass of the ball times its velocity) of both the balls before the collision and after the collision, then the two should be identical. Now, let this experiment be performed on a train where one ball is moving in the same direction as the train, and the other is moving in the opposite direction. An outside observer would say that the initial and final velocities of the balls are one thing, while an observer on the train would say they were something different. However, BOTH observers must agree that the total momentum is conserved. One will say that momentum was conserved because the total momentum before AND after the collision were both some number, A; while the other will say that momentum was conserved because the total momentum before AND after were both some other number, B. They will disagree on what the actual numbers are, but they will agree that the law holds. We should be able to apply this postulate to any physical law. If not, (i.e., if physical laws were different for different frames of reference) then we could change the laws of physics just by traveling in a particular reference frame.
A very interesting result occurs when you apply this postulate to
the laws of electrodynamics (the area of physics which deals with
electricity and magnetism). What one finds is that in order for the
laws of electrodynamics to be the same in all inertial reference
frames, it must be true that the speed of electro-magnetic waves (such
as light) is the same for all inertial observers. Perhaps the easiest
way to explain why this is so is to discuss two constants used in basic
electrodynamics. They are denoted as  and
and
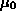 .
. 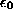 is used in the basic equation
which describes the attraction or repulsion between two electrically
charged particles while
is used in the basic equation
which describes the attraction or repulsion between two electrically
charged particles while 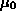 is used in the basic equation
which describes the magnetic force on a charged particle. According
to electrodynamics, these two constants are properties of the
universe, and if any observer in any frame of reference does an
electro-magnetic experiment to measure those constants, he or she must
always come up with the same answers. However, it is also a property
of electrodynamics that the speed (c) of an electro-magnetic wave
(such as light) can be expressed in terms of those two constants:
is used in the basic equation
which describes the magnetic force on a charged particle. According
to electrodynamics, these two constants are properties of the
universe, and if any observer in any frame of reference does an
electro-magnetic experiment to measure those constants, he or she must
always come up with the same answers. However, it is also a property
of electrodynamics that the speed (c) of an electro-magnetic wave
(such as light) can be expressed in terms of those two constants: 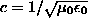 . If
. If
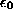 and
and 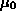 are constants for all inertial
observers, then so is c.
are constants for all inertial
observers, then so is c.
Thus, requiring the laws of electrodynamics to be the same for
all inertial observers suggests that the speed of light should be the
same for all inertial observers. Simply stating that may not make you
think that there is anything that interesting about it, but it has
amazing and far-reaching consequences. Consider letting a beam of
light take the place of the ball in our earlier example (the one where
I was on a train throwing a ball, and you were outside the train). If
the train is moving at half the velocity of light (c), and I say that
the light beam is traveling at the speed c with respect to me,
wouldn't you expect the light beam to look as if it were traveling one
and a half that speed with respect to you? Well, because of the
postulate above, this is not the case, and the old ideas of relativity
in Newton's day fail to explain the situation. All observers must
agree that the speed of any light beam is c, regardless of their frame
of reference. Thus, even though I measure the speed of the light beam
to be c with respect to me, and you see me traveling past you and one
half that speed, still, you must also agree that the light is
traveling at the speed c with respect to you. This obviously seems
odd at first glance, but time dilation and length contraction are what
account for the peculiarity.
1.3 Time Dilation and Length Contraction Effects
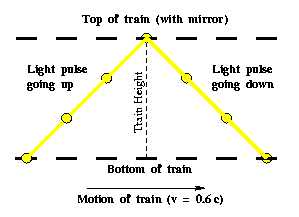
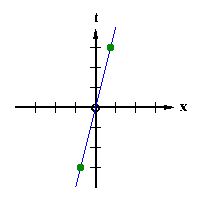
Now, I give an example of how time dilation can help explain a peculiarity that arises from the above concept. Again we consider a case where I am on a train and you are outside the train, but let's give the train a speed of 0.6 c with respect to you. (Note that c is generally used to denote the speed of light which is 300,000,000 meters per second. We can also write this as 3E8 m/s where "3E8" means 3 times 10 to the eighth). Now I (on the train) shine a small burst or pulse of light so that (to me) the light goes straight up, hits a mirror at the top of the train, and bounces back to the floor of the train where some instrument detects it. Now, in your point of view (outside the train), that pulse of light does not travel straight up and straight down, but makes an up-side-down "V" shape because of the motion of the train. This is not just some "illusion", but rather it is truly the way the light travels relative to you, and thus this is truly the way the situation must be considered in your frame of reference. Below is a diagram of what occurs in your frame:
Let's say that the trip up takes 10 seconds in your frame of reference. The distance the train travels during that time is given by its velocity (0.6 c) multiplied by that time of 10 seconds:
(Eq 1:1)
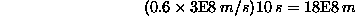
The distance that the light pulse travels on the way up (the slanted line to the left) must be given by its speed with respect to you (which must be c given our previous discussion) multiplied by the time of 10 seconds:
(Eq 1:2)
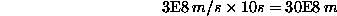
Since the left side of the above figure is a right triangle, and we know the length of its hypotenuse (the path of the light pulse) and one of its sides (the distance the train traveled), we can now solve for the height of the train using the Pythagorean theorem. That theorem states that for a right triangle the length of the hypotenuse squared is equal to the length of one of the sides squared plus the length of the other side squared. We can thus write the following:
(Eq 1:3)
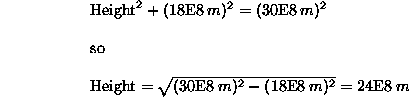
(It is a tall train because we said that it took the light 10 seconds to reach the top, but this IS just a thought experiment.) Now we consider my frame of reference (on the train). In my frame, the light is truly traveling straight up and straight back down to me. This is truly the way the light travels in my frame of reference, and so that's the way we must analyze the situation relative to me. Again, according to our previous discussion, the light must travel at 3E8 m/s as measured by me as well. Further the height of the train doesn't change because relativity doesn't affect lengths perpendicular to the direction of motion. Therefore, we can calculate how long it takes for the light to reach the top of the train in my frame of reference. That is given by the distance (the height of the train) divided by the speed of the light pulse (c):
(Eq 1:4)
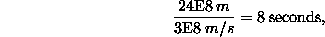
and there you have it. To you the event takes 10 seconds, while according to me it must take only 8 seconds. We measure time in different ways.
You see, to you the distance the light travels is longer than the height of the train (see the diagram). So, the only way I (on the train) could say that the light traveled the height of the train while you say that the SAME light travels a longer distance is if we either (1) have different ideas for the speed of the light because we are in different frames of reference, or (2) we have different ideas for the time it takes the light to travel because we are in different frames of reference. Now, in Newton's days, they would believe that the former were true. The light would be no different from, say, a ball, and observers in different frames of reference can observer different speeds for a ball (remember our first "train" example in this introduction). However, with the principles of Einstein's relativity, we find that the speed of light is unlike other speeds in that it must always be the same regardless of your frame of reference. Thus, the second explanation must be the case, and in your frame of reference, my clock (on the fast moving train) is going slower than yours.
As I mentioned in the last part of the previous section, length contraction is another consequence of relativity. Consider the same two travelers in our previous example, and let each of them hold a meter stick horizontally (so that the length of the stick is oriented in the direction of motion of the train). To the outside observer (you), the meter stick of the traveler on the train (me) will look as if it is shorter than a meter. One can actually derive this given the time dilation effect (which we have already derived), but I wont go through that explanation for the sake of time.
Now, don't be fooled! One of the first concepts which can get into the mind of a newcomer to relativity involves a statement like, "if you are moving, your clock slows down." However, the question of which clock is really running slowly (yours or mine) has no absolute answer! It is important to remember that all inertial motion is relative. That is, there is no such thing as absolute inertial motion. You cannot say that it is the train that is absolutely moving and that you are the one who is actually sitting still.
Have you ever had the experience of sitting in a car, noticing that you seemed to be moving backwards, and then realizing that it was the car beside which was "actually" moving forward. Well, the only reason you say that "actually" the other car was moving forward is because you are considering the ground to be stationary, and it was the other car who was moving with respect to the ground rather than your car. Before you looked at the ground (or surrounding scenery) you had no way of knowing which of you was "really" moving. Now, if you did this in space (with space ships instead of cars), and there were no other objects around to reference to, and neither space ship was accelerating (they were moving at a constant speed with respect to one another) then what would be the difference in saying that your space ship was the one that was moving or saying that it was the other space ship that was moving? As long as neither of you is undergoing an acceleration (which would mean you were not in an inertial frame of reference) there is no absolute answer to the question of which one of you is moving and which of you is sitting still. You are moving with respect to him, but then again, he is moving with respect to you. All motion is relative, and all inertial frames are equivalent.
So what does that mean for us in this "train" example. Well, from my point of view on the train, I am the one who is sitting still, while you zip past me at 0.6 c. Since I can apply the concepts of relativity just as you can (that's the postulate of relativity--all physical laws are the same for all inertial observers), and in my frame of reference you are the one who is in motion, that means that I will think that it is your clock that is running slowly and that your meter sticks are length contracted.
So, there is NO absolute answer to the question of which of our clocks is really running slower than the other and which of our meter sticks is really length contracted smaller than the other. The only way to answer this question is relative to whose frame of reference you are considering. In my frame of reference your clock is running slower than mine, but in your frame of reference my clock is running slower than yours. This lends itself over to what seem to be paradoxes such as "the twin paradox" (doesn't it seem like a paradox that we each believe that the other person's clock is running slower than our own?). Understanding these paradoxes can be a key to really grasping some major concepts of special relativity. The explanation of these paradoxes will be given for the interested reader in
Part II
of this FAQ.
1.4 Introducing Gamma (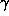 )
)
Now, the closer one gets to the speed of light with respect to an observer, the slower ones clock ticks and the shorter ones meter stick will be in the frame of reference of that observer. The factor which determines the amount of length contraction and time dilation is called gamma (denoted 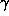 ).
).
Gamma (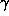 ) for an object moving with speed v in your frame of reference is defined as
) for an object moving with speed v in your frame of reference is defined as
(Eq 1:5)

For our train (for which v = 0.6 c in your frame of reference), 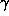 is 1.25 in your frame. Lengths will be contracted and time dilated (as seen by you--the outside observer) by a factor of
is 1.25 in your frame. Lengths will be contracted and time dilated (as seen by you--the outside observer) by a factor of 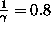 . That is what we demonstrated in our example by showing that the difference in measured times was 10 seconds for you (off the train) and 8 seconds for me (on the train) in your point of view. Gamma is obviously an important number in relativity, and it will appear as we discuss other consequences of the theory (including the effects of special relativity on energy and momentum considerations).
. That is what we demonstrated in our example by showing that the difference in measured times was 10 seconds for you (off the train) and 8 seconds for me (on the train) in your point of view. Gamma is obviously an important number in relativity, and it will appear as we discuss other consequences of the theory (including the effects of special relativity on energy and momentum considerations).
1.5 Energy and Momentum Considerations
Another consequence of relativity is a relationship between mass, energy, and momentum. Note that velocity involves the question of how far you go and how long it takes. Obviously, if relativity affects the way observers view lengths and times relative to one another, one could expect that any Newtonian concepts involving velocity might need to be re-thought. For example, because of relativity we can no longer simply add velocities to transform from one frame to another as we did with the ball and the train earlier. (However, for small velocities like we see every day, the differences which comes in because of relativity are much to small for us to notice).
Further, consider momentum (which in Newtonian mechanics is defined as mass times velocity). With relativity, this value is no longer conserved in different reference frames when an interaction takes place. The quantity that is conserved is relativistic momentum which is defined as
(Eq 1:6)

where gamma (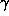 ) is
defined
in the previous section.
) is
defined
in the previous section.
By further considering conservation of momentum and energy as viewed from two frames of reference, one can find that the following equation must be true for the total energy of an unbound particle:
(Eq 1:7)

Where E is energy, m is mass, and p is the relativistic momentum as defined above.
Now, by manipulating the above equations, one can find another way to express the total energy as
(Eq 1:8)

Notice that even when an object is at rest (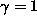 ) it still has an energy of
) it still has an energy of
(Eq 1:9)

Many of you have seen something like this stated in context with the theory of relativity ("E equals m c squared"). It says that because of the relationship between space and time for different observers as discovered by special relativity, we must conclude that an object possesses an internal energy contained in its mass--mass itself contains energy, or, to put it more eloquently, mass is simply a convenient form of energy.
1.5.1 Rest Mass versus "Observed Mass"
It is important to note that the mass, m, in the above equations
has a special definition which we will now discuss (by "mass", we
generally mean the property of an object that indicates (1) how much
force is needed to cause the object to have a certain acceleration and
(2) how much gravitational pull you will feel from that object in
Newtonian gravitation). First, note what happens to the relativistic
momentum (
Equation 1:6
) of an object as its speed approaches c with
respect to some observer. In that observer's frame of reference, its
momentum becomes very large (because 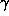 goes to infinity),
especially compared to the old definition of momentum, p = m v. However, if we define a property called "observed mass" as
being
goes to infinity),
especially compared to the old definition of momentum, p = m v. However, if we define a property called "observed mass" as
being 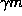 , then we see that the momentum can be
written as
, then we see that the momentum can be
written as
(Eq 1:10)

We see that the momentum can be written exactly as it was in Newtonian
physics, except that it seems the mass of the object as seen by an
outside observer is larger than its "rest mass" (m). Further, if we
take the relativistic equation for the energy of an object,
Equation 1:8
, we see it too can be written as
(Eq 1:11)
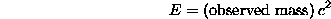
This is like the energy of an object at rest (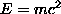 )
with the "observed mass" substituted in for the "rest mass."
)
with the "observed mass" substituted in for the "rest mass."
Thus, one way to interpret relativity's effect on our view of
momentum and energy is to say that because of relativity, an observer
sees an object's mass increase as the object approaches the speed of
light in that observer's frame of reference. The mass (m) in our
equations is thus the mass as measured when the object is at rest in
our frame of reference (the rest mass), not the "observed mass" we
have defined.
However, this concept of observed mass doesn't really work for
gravitational mass. In a relativistic setting, you can't figure out
the gravitational effects of an object that is moving (in your frame)
by simply figuring out what gravitational effects its mass would have
at rest and replacing its mass with the observed mass in your frame
of reference. For example, as the velocity of an object with respect
to you approaches c, its "observed mass" approaches infinity.
However, this does not mean that the object will eventually look like
a black hole predicted by general relativity (as it would if the same
object really did have a huge mass sitting at rest).
Also, let's look at kinetic energy in relation to mass. Kinetic
energy is energy of motion--it's the total energy of a free object
minus the amount of that energy that is internal to the object:
(Eq 1:12)
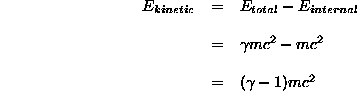
As it turns out, when v is much smaller than c, the equation
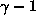 is approximately equal to
is approximately equal to 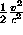 such that
such that 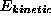 is
approximately
is
approximately 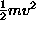 (that's the Newtonian
equation for kinetic energy which is approximately correct for
non-relativistic speeds). But with relativistic velocities, the
kinetic energy becomes much larger than we would have calculated it to
be using the Newtonian equations. In that sense, there does seem to
be some "extra energy" which could be considered as extra mass energy;
however, you can't get the correct kinetic energy in relativity by
simply plugging our expression for "observed mass" into the Newtonian
equation for kinetic energy. The observed mass concept doesn't really
work here, and we see that it's better to simply argue that the mass
isn't really increasing, but rather the equations for energy and
momentum are different than expressed by Newtonian physics.
(that's the Newtonian
equation for kinetic energy which is approximately correct for
non-relativistic speeds). But with relativistic velocities, the
kinetic energy becomes much larger than we would have calculated it to
be using the Newtonian equations. In that sense, there does seem to
be some "extra energy" which could be considered as extra mass energy;
however, you can't get the correct kinetic energy in relativity by
simply plugging our expression for "observed mass" into the Newtonian
equation for kinetic energy. The observed mass concept doesn't really
work here, and we see that it's better to simply argue that the mass
isn't really increasing, but rather the equations for energy and
momentum are different than expressed by Newtonian physics.
So, "observed mass" has its uses, but physicists today rarely
use the concept in practice. Rather, an object is said to have a rest
mass (which truly is its inherent internal energy) as well as an
energy due to its motion with respect to an observer (kinetic energy)
which come together to produce its total energy, E.
1.5.2 The Energy and Momentum of a Photon (Where m = 0)
We should quickly note the case where the rest mass of an object is zero (such is the case for a photon--a particle of light). Given the equation for the energy in the form of
Equation 1:8
(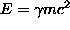 ), one might at first glance think that the energy was zero when m = 0. However, note that massless particles like the photon travel at the speed of light. Since
), one might at first glance think that the energy was zero when m = 0. However, note that massless particles like the photon travel at the speed of light. Since 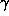 goes to infinity as the velocity of an object goes to c, the equation
goes to infinity as the velocity of an object goes to c, the equation 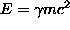 involves one part which goes to zero (m) and one part which goes to infinity (
involves one part which goes to zero (m) and one part which goes to infinity (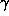 ). Thus, it is not obvious what the energy would be. However, if we use the energy equation in the form of
Equation 1:7
(
). Thus, it is not obvious what the energy would be. However, if we use the energy equation in the form of
Equation 1:7
(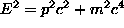 ), then we can see that when m = 0 then the energy is given by E = p c).
), then we can see that when m = 0 then the energy is given by E = p c).
Now, a photon has a momentum (it can "slam" into particles and change their motion, for example) which is determined by its wavelength (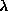 ) in the equation
) in the equation 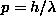 (where
(where 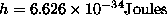 is called Planck's constant). A photon of wavelength
is called Planck's constant). A photon of wavelength 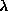 thus has an energy given by
thus has an energy given by 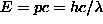 , even though it has no rest mass.
, even though it has no rest mass.
1.6 Experimental Support for the Theory
These amazing consequences of relativity do have experimental foundations. For example, using atomic clocks and super-sonic jets, we have been able to confirm the effects of time dilation just as relativity predicts. Another experimental confirmation involves the creation of particles called muons by cosmic rays (from the sun) in the upper atmosphere. These muons then travel at very fast speeds towards the earth. In the rest frame of a muon, its life time is only about 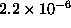 seconds. Even if the muon could travel at the speed of light, it could still go only about 660 meters during its life time. Because of that, they should not be able to reach the surface of the Earth. However, it has been observed that large numbers of them do reach the Earth. From our point of view, time in the muon's frame of reference is running slowly, since the muons are traveling very fast with respect to us. So the
seconds. Even if the muon could travel at the speed of light, it could still go only about 660 meters during its life time. Because of that, they should not be able to reach the surface of the Earth. However, it has been observed that large numbers of them do reach the Earth. From our point of view, time in the muon's frame of reference is running slowly, since the muons are traveling very fast with respect to us. So the 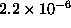 seconds are slowed down, and the muon has enough time to reach the earth.
seconds are slowed down, and the muon has enough time to reach the earth.
We must also be able to explain the result from the muon's frame of reference. In its point of view, it does have only 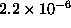 seconds to live. However, the muon would say that it is the Earth which is speeding toward the muon. Therefore, the distance from the top of the atmosphere to the Earth's surface is length contracted. Thus, from the muon's point of view, it lives a very small amount of time, but it doesn't have that far to go. This is an interesting point of Relativity--the physical results (e.g. the muon reaches the Earth's surface) must be true for all observers; however, the explanation as to how it came about can be different for different frames of reference.
seconds to live. However, the muon would say that it is the Earth which is speeding toward the muon. Therefore, the distance from the top of the atmosphere to the Earth's surface is length contracted. Thus, from the muon's point of view, it lives a very small amount of time, but it doesn't have that far to go. This is an interesting point of Relativity--the physical results (e.g. the muon reaches the Earth's surface) must be true for all observers; however, the explanation as to how it came about can be different for different frames of reference.
Another verification of special relativity is found all the time in particle physics. In particle physics, large accelerators push particles to speeds very close to the speed of light, and experimenters then cause those particles to strike other particles. The results of such collisions can be understood only if one uses the momentum and energy equations which were predicted by relativity (for example, one must take the total energy of the particle to be 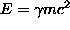 , which was predicted by relativity).
, which was predicted by relativity).
These are only a few examples that give credibility to the theory of relativity. Its predictions have turned out to be true in many cases, and to date, no evidence exists that would tend to undermine the theory in the areas where it applies.
In the above discussion of relativity's effects on space and time we have specifically mentioned length contraction and time dilation. However, there is a little more to it than that, and the next section attempts to explain this to some extent.
Chapter 2: Space-Time Diagrams
In this section we examine certain constructions known as space-time diagrams. After a short look at why we need to discuss these diagrams, I will explain what they are and what purpose they serve. Next we will construct a space-time diagram for a particular observer. Then, using the same techniques, we will construct a second diagram to represent the coordinate system for a second observer who is moving with respect to the first observer. This second diagram will show the second observer's frame of reference with respect to the first observer; however, we will also switch around the diagram to show what the first observer's frame of reference looks like with respect to the second observer. Finally, we will compare the concepts these two observers have of future and past, which will make it necessary to first discuss a diagram known as a light cone.
2.1 What are Space-Time Diagrams?
In the previous section we talked about the major consequences of special relativity, but now I want to concentrate more specifically on how relativity causes a transformation of space and time. Relativity causes a little more than can be understood by simple notions of length contraction and time dilation. It actually results in two different observers having two different space-time coordinate systems. The coordinates transform from one frame to the other through what is known as a Lorentz Transformation. Without getting deep into the math, much can be understood about such transforms by considering space-time diagrams.
2.2 Time as Another Dimension
One of the first points to make as we begin discussing space-time diagrams is that we are treating time as another dimension along with the three dimensions of space. Generally, people aren't used to thinking of time as just another dimension, but doing so allows us to truly understand how relativity works. So, how do we represent time as just another dimension?
Obviously we can't actually picture four dimensions all at once (three of space and one of time). Our minds are limited to picturing the three dimensions of space that we are used to dealing with. However, we can consider one or two dimensions of space and then use another dimension of space to represent time.
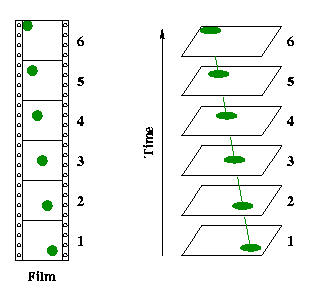
To see how this can work, consider
Diagram 2-1. There you see a film strip on which each frame represents a moment in time. As you watch a film, you see each moment in time presented one right after another, and this gives the impression of seeing time pass. If we cut the film up into frames then we can stack the frames flat, evenly spaced, and one on top of the other (as shown in the diagram). Then each frame is a two dimensional representation of space and as you move through the third dimension you go up the stack, and each frame you pass represents another point in time. Thus, we have a three dimensional stack which represents two dimensions of space and the third dimension represents time.
Note too that in the diagram the film shows a ball moving from one corner of the screen to the other. However, in the three dimensional stack, the ball now follows a three dimensional path through space-time. In four dimensional space-time, objects which we see moving in time through three dimensional space are following a four-dimensional path through space-time. On space-time diagrams, paths you draw represent objects moving through space as time passes, but we'll see more about that later in the chapter.
Further, consider an event such as "the ball reaches the far corner of the screen." That is a single event--it occurs at one moment in time and at one particular place in space. On our diagram, it is a single point (it is a spot represented by the ball which is on the upper most frame in the stack). Any single event which occurs is represented by a single point on a space-time diagram.
And so, a space-time diagram gives us a means of representing events which occur at different locations and at different times. Every event is portrayed as a point somewhere on the space-time diagram.
Now, because of relativity, different observers which are moving relative to one another will have different coordinates for any given event. However, with space-time diagrams, we can picture these different coordinate systems on the same diagram, and this allows us to understand how they are related to one another.
2.3 Basic Information About the Diagrams we will Construct
In
Diagram 2-1
we saw how one can use three dimensions to represent two dimensions of space and one of time, but for simplicity the diagrams we use will be two dimensional--one of space and one of time. We will consider the one dimension of space to be the x direction. So, the space-time diagram consists of a coordinate system with one axis to represent space (the x direction) and another to represent time. Where these two principal axes meet is the origin. This is simply a point in space that we have defined as x = 0 and a moment in time that we have defined as t = 0. In
Diagram 2-2
(below) I have drawn these two axes and marked the origin with an o.
For certain reasons we want to define the units that we will use for distances and times in a very specific way. Let's define the unit for time to be the second. This means that moving one unit up the time axis will represent waiting one second of time. We then want to define the unit for distance to be a light second (the distance light travels in one second). So if you move one unit to the right on the x axis, you will be considering a point in space that is one light second away from your previous location. In
Diagram 2-2
, I have marked the locations of the different space and time units.
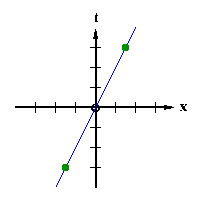
With these units, it is interesting to note how a beam of light is represented in our diagram. Consider a beam of light leaving the origin and traveling to the right. One second later, it will have traveled one light second away. Two seconds after it leaves it will have traveled two light seconds away, and so on. So a beam of light will always make a line at an angle of 45 degrees to the x and t axes. I have drawn such a light beam in
Diagram 2-3.
2.4 Constructing One for a "Stationary" Observer
At this point, we want to decide exactly how to represent events on this coordinate system for a particular observer. First note that it is convenient to think of any particular space-time diagram as being specifically drawn for one particular observer. For
Diagram 2-2
, that particular observer (let's call him the O observer) is the one whose coordinate system has the vertical time axis and horizontal space axis shown in that diagram. Now, other frames of reference (which don't follow those axes) can also be represented on this same diagram (as we will see). However, because we are used to seeing coordinate systems with horizontal and vertical axes, it is natural to think of this space-time diagram as being drawn specifically with the O observer in mind. In fact, we could say that in this space-time diagram, the O observer is considered to be "at rest".
So if the O observer starts at the origin, then one second later he is still at x = 0 (because he isn't moving in this coordinate system). Two seconds later he is still at x = 0, etc. If we look at the diagram, we see that this means he is always on the time axis in our representation. Similarly, any lines drawn parallel to the t axis (in this case, vertical lines) will represent lines of constant position. If a second observer is not moving with respect to the first, and this second observer starts at a position two light seconds away to the right of the first, then as time progresses he will stay on the vertical line that runs through x = 2.
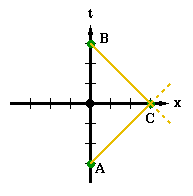
Next we want to figure out how to represent lines of constant time. We might first find a point on our diagram that represents an event which occurs at the same time as, say, the origin (t = 0). To do this we will use a method that Einstein used. First we choose a point on the t axis which occurred prior to t = 0. Let's use an example where this point occurs at t = -3 seconds. At that time we send out a beam of light in the positive x direction. If the beam bounces off of a distant mirror at t = 0 and heads back toward the t axis, then it will come back to the us at t = 3 seconds. We know this because (1) it will have traveled for three seconds away from us, (2) it will have the same distance to travel back to us in our frame of reference, and (3) according to relativity it must travel at the same speed, c, going and coming back. Thus, it must take three seconds to get back to us as well which means it reaches as at the time t = 3 seconds. So, if we send out a beam at t = -3 seconds and it returns at t = 3 seconds, then the event "it bounced off the mirror" occurred simultaneously with the time t = 0 at the origin.
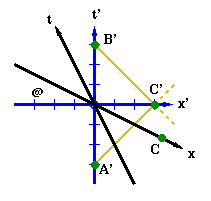
To use this on our diagram, we first pick the two points on the t axis that mark t = -3 and t = 3 (let's call these points A and B respectively). We then draw one light beam leaving from A in the positive x direction. Next we draw a light beam coming to B in the negative x direction. Where these two beams meet (let's call this point C) marks the point where the original beam bounces off the mirror. Thus the event marked by C is simultaneous with t = 0 (the origin). A line drawn through C and o will thus be a line of constant time. All lines parallel to this line will also be lines of constant time. So any two events that lie along one of these lines truly occur at the same time in this frame of reference. I have drawn this procedure in
Diagram 2-4
, and you can see that the x axis is the line through both o and C which is a line of simultaneity (as one might have expected).
Note that the event marked by C is not seen by the O observer (who, remember, is represented by the t axes because he sits at x = 0) at the moment it happens (t = 0) but it is seen once light from C reaches the O observer (which is the point marked B). However, because of the way we did the experiment, we know that in this frame of reference, C truly did happen simultaneously with the origin, o. This just goes to illustrate, as discussed in
Section 1.1
, that when I say that two events happened simultaneously in some frame of reference, I am not talking about when they are seen by some observer in that frame. Rather, I am talking about when they actually occur in that frame of reference. On our diagrams, events are represented at their actual space-time locations relative to one another, and in a particular frame of reference that means that we show exactly when and where the event occurred (not "observed" but truly occurred) in that frame.
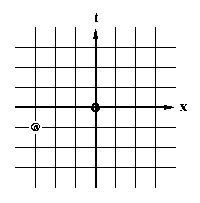
Now, by constructing a set of simultaneous time lines and constant position lines we will have a grid on our space-time diagram. Any event has a specific location on the grid which tells where and when it occurs in this frame of reference. In
Diagram 2-5
I have drawn one of these grids and marked an event (@) that occurred 3 light seconds away to the left of the origin (x = -3) and 1 second before the origin (t = -1).
2.5 Constructing One for a "Moving" Observer
Now comes an important addition to our discussion of space-time diagrams. The coordinate system we have drawn will work fine for any observer who is not moving with respect to the O observer. Now we want to construct a coordinate system for an observer who IS traveling with respect to the O observer. The trajectories of two such observers have been drawn in
Diagram 2-6
and
Diagram 2-7. Notice that in our discussion we will usually consider moving observers who pass by the O observer at the time t = 0 and at the position x = 0. Thus, the origin will mark the event "the two observers pass by one another".
Now, the traveler in
Diagram 2-6
is moving slower than the one in
Diagram 2-7. You can see this because in a given amount of time (distance along the t axis), the Diagram 2-7 traveler has moved further away from the time axis than the Diagram 2-6 traveler. So the faster a traveler moves, the more slanted this line becomes.
What does this line actually represent? Well, remember that the line marks the position of our observer at different times on our diagram. But, also, consider an object sitting right next to our moving observer. If a few seconds later the object is still sitting right next to him (practically on that line), then, in his point of view, the object has not moved. So, the line is a line of constant position for the moving observer. Nothing on that line is moving with respect to him. But that means that this line represents the same thing for the moving observer as the t axis represented for the O observer; and in fact, this line becomes the moving observer's new time axis. We will mark this new time axis as t' (t-prime). All lines parallel to this slanted line will also be lines of constant position for our moving observer.
Now, just as we did for the O observer, we want to construct lines of constant time for our traveling observer. To do this, we will use the same method that we did for the O observer. The moving observer will send out a light beam at some time t'= -T, and the beam will bounce off some mirror so that it returns to him at time t'= +T. Now remember, light travels at the same speed in any direction for all observers, so our traveling observer must conclude that the light beam took the same amount of time traveling out as it did coming back in his frame of reference. If in his frame the light left at t'= -T and returned at t'= +T, then the point at which the beam bounces off the mirror must have occurred simultaneously with the origin, where t'= t = 0, in the frame of reference of our moving observer.
There is a very important point to note here. What if instead of light, we wanted to throw a ball at 0.5 c, have it bounce off some wall, and then return at the same speed (0.5 c). The problem with this is that to find a line of constant time for the moving observer, the ball must travel at 0.5 c both ways in the reference frame of the moving observer. But we have not yet defined the coordinate system for the moving observer, so we do not know what a ball moving at 0.5 c with respect to him will look like on our diagram. However, because of relativity, we know that the speed of light itself cannot change from one observer to the next. In that case, a beam of light traveling at c in the frame of the moving observer will also be traveling at c for the O observer. So, a line which makes a 45 degree angle with respect to the x and t axes will always represent a beam of light traveling at speed c for any observer in any frame of reference.
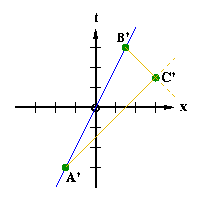
In
Diagram 2-8
, I have labeled a point A' on the t' axes which occurs some amount of time before t'= 0 and a point B' which occurs the same amount of time after t'= 0. I then drew the two light rays (remember, these are "45 degree angle" lines) as before--one leaving from A and going to the right, and one moving to the left and coming in to B. I then found the point where they would meet (C') which marks the point where the ray from A' would have had to bounce in order to get back to the moving observer at B'. Thus, C' and o occur at the same time in the frame of the moving observer. Notice that for the O observer, C' is above his line of simultaneity at o (the x axis). So while the moving O' observer says that C' occurs when the two observers pass (at the origin), the O observer says that C' occurs after the two observers have passed by one another. We will further discuss this difference in the concepts of future and past in
Section 2.8.
In
Diagram 2-9
, I have drawn a line passing through C' and o. This line represents the same thing for our moving observer as the x axis did for the O observer. So we label this line x'.
From the geometry involved in finding this x' axis, we can state a general rule for finding the x' axis for any moving observer. First recall that the t' axis is the line that represents the moving observer's position on the space-time diagram. The faster O' is moving with respect to O, the greater the angle between the t axis and the t' axis. So the t' axis is rotated away from the t axis at some angle (either clockwise or counterclockwise, depending on the direction O' is going--right or left). The x' axis is then a line rotated at the same angle away from the x axis, but in the opposite direction (counterclockwise or clockwise).
Now, x' is a line of constant time for O', and any line drawn parallel to x' is also a line of constant time. Such lines, along with the lines of constant position, form a grid of the space-time coordinates for the O' observer. I have tried my best to draw such a grid in
Diagram 2-10. If you look at that diagram, you can see the skewed squares of the coordinate grid. You can see that if you pick a point on the space-time diagram, the two observers with their two different coordinate systems will disagree on when and where the event occurs.
As a final note about this procedure, think back to what really made these two coordinate systems look differently. Well, the only thing we assumed in creating these systems is that the speed of light is the same for all observers. In fact, this is the only reason that the two coordinate systems look the way they do.
2.6 A Quick Comparison of the two Observers
For a moment, I want to go back and compare the two observers in
Diagram 2-8. Consider how the O observer would explain the experiment done by the O' observer. First note that in the coordinate system used by the O observer, the point marked C' is above the x axis. This means that in the O observer's frame of reference, C' happens after the origin (when the two observers pass by one another). However, we concluded that for O' the C' event happens at the same time as the two observers are passing one another. What does that mean?
Look at the parts of the experiment O' did (including the actions of O' and the events A', B', and C') as they appear in the O observer's frame. In that frame, O' sends out a light signal when his own clock reads t' = -T, but note also that he is moving along with that signal (according to O). The distance between them changes slowly at the beginning according to O because O' is moving along with the signal in the same direction. Then, according to O, the two observers pass by one another. Next, the C' event happens and the light bounces back toward the two observers. In the frame of the O observer, the O' observer is now racing towards the light beam, and so the distance between them is changing very quickly. Finally, the light beam reaches O' as his clock is ticking t' = +T.
So, we see that in the O frame of reference, because O' is moving along with the light before C' and is moving towards the light after C' that means C' has to happen after the "half way point" (when the two observers pass one another).
However, relativity says that O' cannot agree with that analysis. In the frame of O', it is the O observer who is moving. Further, O' cannot agree that the distance between him and the light is changing slowly before C' and quickly after C'. Why can't he agree? Well, because then he would measure the speed of the light in his frame of reference and find it to be different going away from him than it is coming back to him. As discussed in
Section 1.2
, relativity dictates that for any inertial observer, when he measures the speed of light he must find the speed to be c--always, and in all directions. If O' has to find that the light is traveling at the same speed going and coming back, then O' also has to conclude that in his frame C' really, truly happens at the same time as the origin (when and where the two observers pass one another). O' thus has a different coordinate system than O, and he measure space and time differently.
And so, in one frame of reference C' really, truly happens after the two observers pass one another, but in another frame of reference C' really, truly happens and the same time the two observer's pass. We find that the notion of simultaneity is relative, and we will discuss this further in just a bit.
Next, though, I want to address a possibility you might be thinking right now. That is, why can't it simply be that O' is just wrong in interpreting things as he does and that O is correct. One might want to claim that the reason O' is confused is that he is moving while O is not. But next we will see that we can interchange the two observers, and it becomes obvious that there is no absolute way to claim that one of them is the "correct" observer.
2.7 Interchanging "Stationary" and "Moving"
In our understanding of space-time diagrams, we need to incorporate the idea that all reference frames that are not accelerating are considered equivalent and that all motion is relative. By this I mean that O was considered as the stationary observer only because we defined him as such. Remember? We said that this it is natural to think of the diagram being drawn specifically for the observer whose coordinate system is drawn with vertical and horizontal axes. We then said that we can think of that observer (O) to be considered "at rest" in this diagram. Then, when I called O' the moving observer, I meant that he was moving with respect to O.
However, we should just as easily be able to define O' as the stationary observer. Then, to him, O is moving away from him to the left. Then, we should be able to draw the t' and x' axes as the vertical and horizontal lines, while the t and x axes become the rotated lines. I have done this in
Diagram 2-11. By examining this diagram, you can confirm that it makes sense to you in light of our discussion thus far. (For example, picture grabbing the x' and t' axes in
Diagram 2-9
and rotating them around the origin until they are horizontal and vertical lines. If x and t follow your rotation, then you can see how they would end up as they are drawn in
Diagram 2-11.)
I have also included in
Diagram 2-11
the experiment that O' did in which he decided how to draw the x' axis, and you can see that it now looks just like the experiment O did when his x and t axes were the horizontal and vertical lines. Further in
Diagram 2-11
you can see that the experiment done by the O observer now looks like the one which has incorrectly concluded that C occurs at the same time the two observers are passing one another.
Thus, you can see that we can completely interchange the concept of which observer is moving and which is sitting still, and as a result we must conclude that neither frame of reference is any "better" than the other. When O concludes that C occurs simultaneous with o, he is really, truly correct for his frame of reference. Also, when O' concludes that it is C' which occurs simultaneous with o, he is also really, truly correct for his frame of reference. The notion of simultaneity is not absolute, but really, truly depends on your frame of reference. To understand why this doesn't cause contradictions, we go to the next section in which we discuss the notion of future and past with relativity in mind.
2.8 "Future", "Past", and the Light Cone
For the later FTL discussions, it will be important to understand the way different observers have different notions concerning the future and the past. This difference comes about because of the way the different coordinate systems of the two observers compare to one another.
First, let me note that with what we have discussed we cannot make a complete comparison of the two observers' coordinate systems. You see, we have not seen how the lengths which represents one unit of space and time in the reference frame of O compare with the lengths representing the same units in O'. This will be covered in the Part II: More on Special Relativity (which is "optional" for those of you just interested in the faster than light discussions). We can, however, compare the observers' notions of future and past.
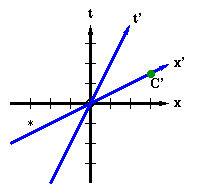
Back on
Diagram 2-9
, in addition to the O and O' space and time axes, I also marked a particular event with a star, "*". Recall that for O, any event on the x axis occurs at the same time as the origin (the place and time that the two observers pass each other). Since the marked event appears under the x axis, then O must find that the event occurs before the observers pass each other in his frame. Also recall that for O', those events on the x' axis are the ones that occur at the same time the observers are passing. Since the marked event appears above the x' axis, O' must find that the event occurs after the observers pass each other in his frame. So, when and where events occur with respect to other events is completely dependent on ones frame of reference. Note that this is not a question of when the events are seen to happen in different frames of reference, but it is a question of when they really do happen in the different frames (recall our discussion of reference frames in
Section 1.1
). So, how can this make sense? How can one event be both in the future for one observer and in the past for another observer. To better understand why this situation
doesn't contradict itself, we need to look at one other construction typically shown on a space-time diagram.
In
Diagram 2-12
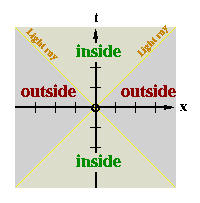
I have drawn two light rays, one which travels in the +x direction and another which travels in the -x direction. At some negative time, the two rays were headed towards x = 0. At t = 0, the two rays finally get to x = 0 and cross paths (at the origin). As time progresses, the two then speed away from x = 0. This construction is known as a light cone.
A light cone divides a space-time diagram into two major sections: the area inside the cone and the area outside the cone (as shown in
Diagram 2-12
). (Let me mention here that I will specifically call the cone I have drawn "a light cone centered at the origin", because that is where the two beams meet.) Now, consider an observer who has been sitting at x = 0 (like our O observer) and is receiving and sending signals at the moment marked by x = 0, t = 0 (at the origin). Obviously, if he sends out a signal, it proceeds away from x = 0 into the future, and the event marked by someone receiving the signal would be above the x axis (in his future). Also, if he is receiving signals at t = 0 , then the event marked by someone sending the signal would have to be under the x axis (in his past). Now, if it is impossible for anything to travel faster than light, then the only events occurring before t = 0 that the observer can know about at the moment are those that are inside the light cone. Also, the only future events (those occurring after t = 0) that he can influence are, again, those inside the light cone.
Now, one of the most important things to note about a light cone is that its position is the same for all observers (because the speed of light is the same for all observers). For example, picture taking the skewed coordinate system of the moving observer and superimposing it on the light cone I have drawn (note: a diagram which shows this view will be given in
Part II: More on Special Relativity
). If you were to move one unit "down" the x' axis (a distance that represents one light second for our moving observer), and you move one unit "up" the t' axes (one second for our moving observer), then the point you end up at should lie somewhere on the light cone. In effect, a light cone will always look the same on our diagram regardless of which observer is drawing the cone.
This fact has great importance. Consider different observers who are all passing by one another at some point in space and time. In general, they will disagree with each other on when and where different events had and will occur. However, if you draw a light cone centered at the point where they are passing each other, then they will ALL agree as to which events are inside the light cone and which events are outside the light cone. So, regardless of the coordinate system for any of these observers, the following facts remain: The only events that any of these observers can ever hope to influence are those which lie inside the upper half of the light cone. Similarly, the only events that any of these observers can know about as they pass by one another are those which lie inside the lower half of the cone. Since the light cone is the same for all the observers, then they all agree as to which events can be known about as they are passing and which can be influenced at some point after they pass.
Now let's apply this to the observers and event in
Diagram 2-9. As you can see, the marked event is indeed outside the light cone. Because of this, even though the event is in one observer's past at the time in question (t = t'= 0), he cannot know about the event at the time. Also, even though the event is in the other observer's future at the time, he can never have an effect on the event after. In essence, the event (when it happens, where it happens, how it happens, etc.) is of absolutely no consequence for these two observers at the time in question. As it turns out, anytime you find two observers who are passing by one another and an event which one observer's coordinate system places in the past and the other observer's coordinate system places in the future, then the event will always be outside of the light cone centered at the point where the observers pass.
But doesn't this relativistic picture of the universe still present an ambiguity in the concepts of past and future? Perhaps philosophically it does, but not physically. You see, the only time you can see these ambiguities is when you are looking at the whole space-time picture at once. If you were one of the observers who is actually viewing space and time, then as the other observer passes by you, your whole picture of space and time can only be constructed from events that are inside the lower half of the light cone. If you wait for a while, then eventually you can get all of the information from all of the events that were happening around the time you were passing the other observer. From this information, you can draw the whole space-time diagram, and then you can see the ambiguity. But by that time, the ambiguity that you are considering no longer exists. So the ambiguity can never actually play a part in any physical situation. Finally, remember that this is only true if nothing can travel faster than the speed of light.
Well, that concludes our introduction to special relativity and space-time diagrams. The next section deals with these concepts with more detail; however, if the reader wishes to skip to the FTL discussion, the information provided in the above sections should be enough to follow that discussion.
|FTL Homepage|
----
|Intro
|Part I
|Part II
|Part III
|Part IV|
----
|Other Versions|
|My Homepage|
|Physics and Star Trek|
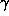 )
)